Dan Meyer’s work on mathematical modeling has been instrumental in shaping my own understanding. I’m super thankful for Dan’s commitment to SMP #4 over the years.
So when he recently posted that he was shifting gears, I was bummed. It was like the pizza was snatched from the fat kid and he wasn’t done eating.
Unfortunately there’s little research on elementary modeling. So as I collect my thoughts on virtual paper, I’m open to any suggestions as to what mathematical modeling is, and what should it look like through the eyes of an elementary teacher.
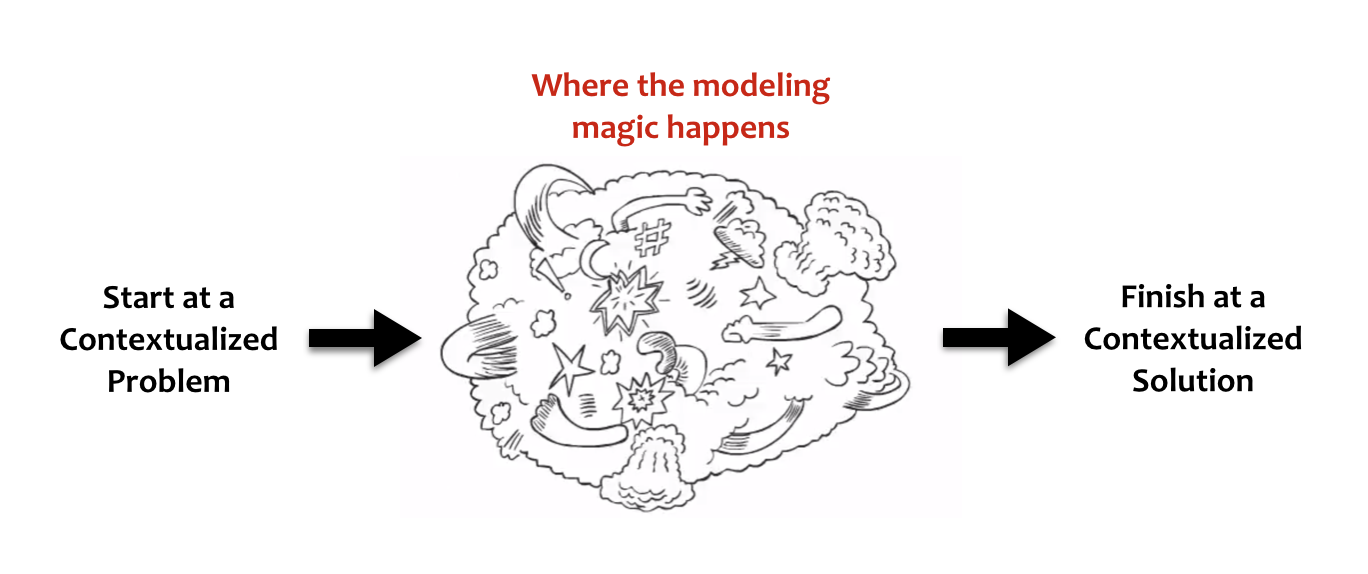
1.Without a context SMP #4 doesn’t exist: The use of manipulatives alone does not constitute modeling. This is the biggest misconception I repeatedly encounter when discussing this standard with teachers. There must be a context in order for mathematical modeling to take place. Modeling is everything that happens in-between the start and the finish.
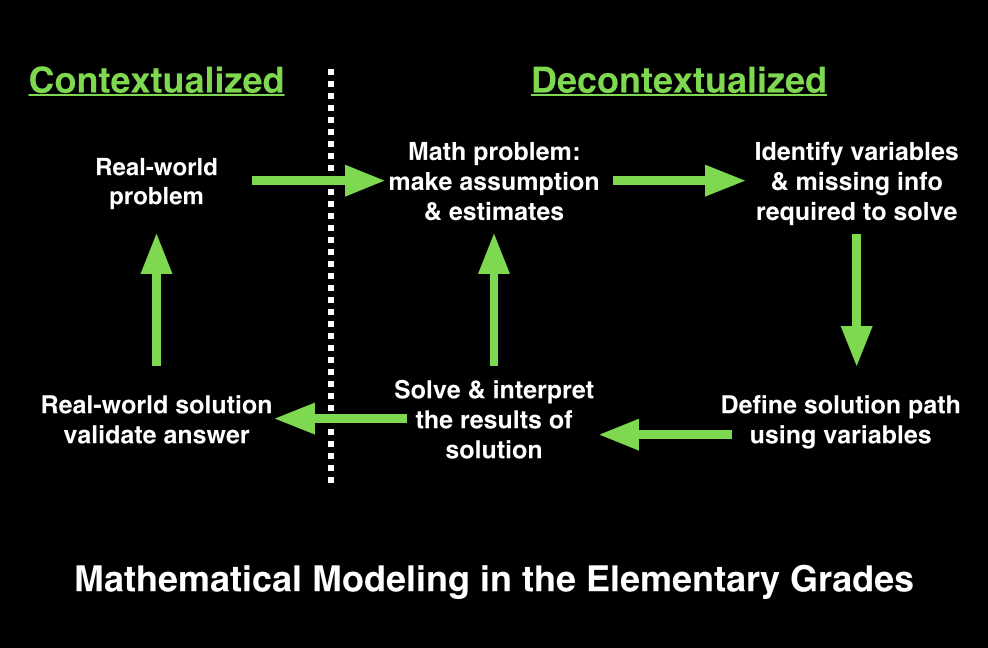
2.The mathematics must be decontextualized: This means that students are looking at the initial problem and identifying key variables. Decontextualized mathematics means that variables have been extrapolated from problem and are now just numbers void of context. Once students have grappled with the numbers and determined a solution, they throw them back into context to assess the reasonableness of their solution. Does it fit? Does it make sense?
3.If you tell the students the information they need to solve the problem upfront…it’s not modeling. Students must identify the variables. I think if we start here as elementary teachers our students will be far better off. Joe Schwartz has one of the best posts I have read on this idea entitled What if we took the problem apart and put it back together again?
In Dan’s most recent article, he discusses the components of mathematical modeling:
- Identifying essential variables in a situation
- Formulating models from those variables
- Performing operations using those models
- Interpreting the results of those operations
- Validating the conclusions of those results
- Reporting the conclusion
Here’s how modeling flows in AND out of context.
Let’s not kid ourselves, it can be extremely difficult and frustrating at times to have 6 & 7 year olds engage in the modeling process. We might not get through the entire process in one or two classes…. and that’s ok. What I believe is most important is that we’re creating mathematical residue which is worth its weight in gold.
Exposure and opportunity to explore the components of modeling is what I’m personally after. Maybe not all of them every time…but definitely more than our track record shows. The bits and pieces of modeling should be woven into our everyday practice.
Bill McCallum and the wonderful people at Illustrative Mathematics do an excellent job laying out the SMPs in the K-5 Elaborations of the Practice Standards. Sure classroom posters are cute, but we need to ensure our own understanding isn’t watered down.
What’s your thoughts on modeling in the elementary grades? What’s worked? What hasn’t? Where did I miss the mark?
Trying to make complex concepts digestible for kids in the elementary grades is such a creative challenge, whether you’re teaching math modeling or introducing them to digital skills. Visual aids are everything when keeping young minds engaged. I actually started using basic image projects to help my kids visualize data and stories, but finding simple tools was tough. This article on why Luminar is the best choice for beginners in photo editing https://skylum.com/blog/why-luminar-is-the-best-choice-for-beginners-in-photo-editing ended up being a fantastic resource for us. It keeps things intuitive without a steep learning curve, making it perfect for creative classroom projects.
“So when he recently posted that he was shifting gears, I was bummed. It was like the pizza was snatched from the fat kid and he wasn’t done eating.”
You’re up, Graham!
Trying to make complex concepts digestible for kids in the elementary grades is such a creative challenge, whether you’re teaching math modeling or introducing them to digital skills. Visual aids are everything when keeping young minds engaged. I actually started using basic image projects to help my kids visualize data and stories, but finding simple tools was tough. This article on why Luminar is the best choice for beginners in photo editing https://skylum.com/blog/why-luminar-is-the-best-choice-for-beginners-in-photo-editing ended up being a fantastic resource for us. It keeps things intuitive without a steep learning curve, making it perfect for creative classroom projects.
Wow. I really like the way you synthesized this. In particular, “without a context SMP #4 doesn’t exist” is really short and sweet. It is a really easy way to check yourself if you think you are doing math modeling. Also, I’m sure that you realize your second point aligns perfectly with math practice #2.
Great stuff. Really well laid out.
Thanks Robert! You answered a lot of the questions I had in regards to modeling when you visited with our DOE and used Andrew’s “File Cabinet”. You were a huge help!
Funny how the more we unpack and truly dive into our own understanding of the SMPs, the more we realize that none of them can really stand alone in isolation.
Another great post, Graham. I like the image of mathematical residue. howardat58’s comment that, “…one of the key features of a real problem is that the context contains at least one criterion for acceptability of a proposed solution which is not, or not particularly, quantitative” is really thought provoking, especially in an elementary (specifically primary) context. I have similar thoughts as Simon, that I don’t think I’ve ever hit a modeling sweet spot (His fruit juice carton exploration is amazing). Maybe circled around it but not really gotten there.
Howard’s comments and the post I shared in SImon’s reply have me reevaluating my thinking. This might be something the 3 of us need to knock around for a bit until we can flesh out and example. Time to go “sweet spot” fishing!
I think your model of modelling is spot-on, Graham. Thing is, I want to do it, but I’m not sure I’m there yet, don’t think I’m really doing it.
Perhaps our ‘design a carton to hold a litre of juice” had elements of modelling in it.
http://y4ist.blogspot.fr/search/label/carton
But, I had to hold their hands too much. They needed – so it seemed to me – pointers too often.
That stage of abstraction, of finding the key analogue that simplifies the situation, I’d like the class to be doing that. Then they’re going to have to process that mathematically somehow. And then convert it back into real-world proposals or description. So, it needs to be within their ability to tackle a lot of that independently.
What I’d really like – being kind of lazy, or unimaginative, I suppose, is someone to just give me a great situation or problem that 8 / 9 year olds can model. In fact, I think we’d all benefit from seeing some really good examples.
So, if you or your readers have got one or two, I’d love to see them. (I won’t promise to use it either – sorry – it’s got to play out with my idiosyncratic mind for me to take it on. There: I’m asking for a gift, and looking the gift horse in the mouth before it even arrives!)
After reading Joe Plesko’s post on modeling with mathematics (http://modelwithmathematics.com/2015/08/is-this-mathematical-modeling/) I have more questions than answers. I even think that 3-Act tasks fall short of true mathematical modeling for the reason that there’s only one answer and students are not given the option of identifying the model that “fits best”. I see them more as micro-modeling opportunities.
I really like your “Juice Box” task and I wouldn’t be too put off by the fact that you had to lend a hand. I’m wondering what the initial question was that drove the work. I’m sorry if I missed it. (ie: What is the least amount of paper that could be used to hold a litre of juice?)
I’m going to shift my thinking to find more opportunities for elementary students to work through the full modeling process. As I find or create them I’ll be sure to pass along. One thing I’m seeing right away is that true modeling can’t be wrapped up in one lesson.
Thanks for pushing my thinking Simon!
In the big outside world people use math to get answers to real problems, and one of the key features of a real problem is that the context contains at least one criterion for acceptability of a proposed solution which is not, or not particularly, quantitative. In other words, a good solution is one which produces pleasure, or satisfaction, or makes the workforce work better, and so on.
One of the best of Dan’s projects involved creating a disk, and the interesting bit was “How do we define a disk”.
I am quite sure that sharing pizzas can be associated with measures of acceptability to the recipients.
Criteria can often be set as vague requirements, “Is it big enough?”, “Will we get there in time?”, “Have we got enough cloth/paper/time to do the job well enough?”. and real discussion and argument will probably result. This is what modeling is all about.
When chance is involved things can get quite heated.
I’m really diggin the idea of vague requirements. I’ve never really thought about it in terms of that. You brought up a really good point which has me definitely reflecting on my own practice.
Too many times I’ve looked at focusing on the measurability of ideas which in turn doesn’t allow for students to compare the effectiveness of each model. To this point, they’ve just shared solutions strategies. Comparing the efficiency and effectiveness of each model is where the magic happens in the closing. Thanks for throwing this in the mix Howard. It’s definitely something I’m going to try and incorporate.
I’m continually talking about trying to start a math fight in class but I might not of been providing my students with the right types of opportunities. You definitely have me questioning my metacognition 🙂 thanks my friend
This is great! Would love to keep thinking about modeling, and what it looks like for young children, with you! I would agree that this practice is highlighting making sense of real world situations through a mathematical lens. So there has to be a context to make sense of and there has to be space for children to bring their own mathematical ideas to the context.
I have a wondering… For our very youngest learners, what does modeling look like? One of the early mathematical ideas they develop is counting. Can we see counting as modeling? They are bringing mathematical ideas (number, counting principles, structure of base-ten) to a real-life context: finding out how many? What do you think?
Also, I’ve just started collecting resources related to modeling and other topics here: https://kendralomax.wordpress.com/favorite-things/resources. Please feel free to add any more that you know of!
Absolutely Kendra and thanks for sharing this resource.
I definitely consider counting to be modeling. When students are adding ones through counting they are employing their understanding of hierarchical inclusion. When we have primary students place counters in a 10 frame to fill it up they are Modeling with Mathematics. The missing piece is when students don’t draw a picture or represent their model as an equation. Without that piece the modeling process is only partially complete. Peas in a Pod and Shark Bait are 2 tasks which I believe gets at the modeling we’re talking about here.
One of the most difficult things I regularly encounter is how to get students to ask the measurable question. That’s why I really love using Andrew’s EST180 with primary students. They’re given the question but then asked to identify the variables and choose the tool they feel is most appropriate.