UPDATE 3/17/19: The updated cards can be found in this post (Multiplication Subitizing Cards: An Upgrade to Building Fluency)
——————————
Learning basic facts through tricks or a mnemonic song lead students down a path of memorization, not understanding. I previously discussed the idea of conceptual development here. When students practice their multiplication facts, they’re expected to move from concrete to abstract too quickly. This takes time!!!
Moving too quickly forces memorization and avoids any possibility of multiplicative thinking. First students are asked to model 3 rows of 6 using colored tiles…
Then after a day or two of exploring arrays, students are magically expected to remember that…
Intensions are good but strategy development is the key underpinning of automaticity. In the past I’ve asked myself the following questions:
- When do students practice multiplication that’s not written as AxB? (for the purpose of automaticity)
- When/how is multiplicative reasoning fostered?
- When do multiplication strategies become automatized?
- When do number strategies become number knowledge?
My answer to all 4 questions….I use multiplication subitizing cards with my daughter whose in 2nd grade so I figured I’d videotape and share.
My takeaways:
- It’s easy to identify which facts she’s comfortable with and has automatized.
- At 1:15– she demonstrates how she used multiplicative thinking for 6×6.
- At 2:00- she could use her understanding of the commutative property for multiplication to build fluency. She was quickly is able to recognize that 7×5=35 at 1 minute, but it took some time to figure out 5×7. She owns this strategy for addition so I’m waiting for it to click with multiplication….no rush:-)
- At 2:20– I missed a fact when she was wrong (doh!)
- At 2:48 and 3:55 she explains her multiplicative reasoning.
5 minutes spent purposefully building fluency and I gained so much information about my daughter. The great thing is that it works for every 8 year old…even the ones in your school.
Disclaimer: I didn’t create the cards and don’t know who did but they deserve a virtual math hug! If you know who did please let me know so I can give proper attribution!
Cheers!


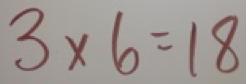
Olá . Não consegui abrir nenhum link. Se puder mande por email.
Quick question.
The cards only go up to 7×7.
Is there a reason for that, or is it a space issue?
I have finished creating some new cards that go up to 9. I’ll share them later this week.
Thanks for such a quick response! I have some kiddoes that just need to develop their multiplication skills.
The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Hey Graham! Did you end up adding the 8’s and 9’s to the subitizing cards? Just wondering where I could find them. These are so great for building conceptual understanding and perfect for Number Talks. Thanks!
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
I am not finding where you uploaded the remainder of the cards. Can you post a new link? Thank you!
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Have these cards been posted somewhere yet?
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Thanks for these resources! Did you publish the subitizing cards that go up to 9? If so, I would love to share them with the teachers I work with.
Thank you!
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Do you have the cards that go through 9’s? My 3rd grade class loves them!
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
I don’t see the added cards… maybe I am missing something. Can you please advise where to look? Thank you!
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Where can I find the updated cards that include 8’s and 9’s? Thanks!
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Hi Graham, are the new cards you created going to be shared on this page or a different page?
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Where can I find the cards for 8s and 9s?
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Where can I find the subitizing cards that include 8’s and 9’s?
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Hi, just wondering if you have uploaded the full set of cards yet? I would love to use them with my class 🙂
Finally!!! The updated cards can now be found in this post: https://gfletchy.com/2019/03/17/multiplication-subitizing-cards/
Thank you for these reminders and ideas. We are using them at our family conferences. I put together a quick “how-to” to accompany the cards. It’s a work-in-progress, but hopefully a helpful start for providing guidance for families. https://goo.gl/xLFpt7
Thank you Tara for the “how-to” document! I am in the middle of parent conferences and have been explaining how to use these cards at every single one. It will be great to be able to send this home so they have something to reference. You are awesome!
Just a thought…. At my school, our students are familiar with the structure of the ten frame and use them to compose and decompose numbers concretely when adding and subtracting. I recently started working with students in a third grade classroom and discovered that the only way they would solve a multiplication problem was to skip count. I wanted to push students to discover other strategies, so I thought, why not use the ten frame structure for fostering multiplication fluency? First they used the ten frame for 2’s facts (instead of counting by 2’s) and they quickly made the connection of x 2 being the same as adding doubles from first and second grade. Next they started representing 4’s facts on the ten frame. When I asked them what 4 x 9 was, some kids said it was too hard and started skip counting (unsuccessfully). I asked them to use the ten frame to represent 4 x 9 … you should have seen the kids as they figured out the answer! I had kids wide eyed and jumping up and down, excited to share what they saw! Students explained that they knew 4 x 9 = 36 because they could see that it was one group of 4 less than 4 x 10 (40-4=36). They tested their theory with other factors and 9 and soon realized that they could figure out any number multiplied by 9 because the answer is one group (of that factor) less than than that factor times ten.
Just my 2 cents on the topic of fact fluency. Give kids opportunities to play and explore with numbers concretely and they will learn their math facts (all operations) quicker than if we drill flash cards at them all day. Plus, I think that if kids play with numbers they get to see relationships among numbers, which helps them in all aspects of the math curriculum – I’m thinking about the connection between multiplication and division AND fractions. If kids memorize their facts (vs. learning them), I don’t think that they make connections and that makes understanding division and fractions so much more difficult.
Can you explain why some of the boxes are blacked out at the end of the document? I’m new to subitizing. Thanks! Happy to have found this resource!
I love the covered up boxes. It forces students to believe that there are equal amounts in each group, and the do not have to count every single dot on the card. Instead, if they need to count, they are to just know how many are in each grouping.
Do you have the cards available to print and use?
There’s a hyperlink just above the video. Click that and you will get the goods.
Hey can you explain exactly what there use is please?
Are okay to be used daily?
Thanks
Colin.
Teachers use them a variety of ways. I think you could use them everyday or once a week if you wanted to. If you’re familiar with Number Talks, these would definetely supplement the thinking that takes place in that space.
Can anyone explain to me why the cards use a different pattern for the smaller pattern of 7 dots inside the circle vs the 7 circles of dots ? To me it does not make sense to have 2 different patterns at micro/macro level.. This is really cool stuff – I will try on my kids (and myself)
Good question Fredrik and to be honest I’ve never really thought about it, but I have noticed it.
I am in the process of creating some similar cards since I am not the one who created these in the first place. I wish I knew who was the creator. I’ll be sure to keep the pattern consistent throughout to help build automaticity. Thanks for pointing that out again.
There are actually a couple of things that was counterintuitive for me:
1. As pointed out – the lack og consistency between micro/macro level
2. Lack of symmetry (I cannot provide a good reason, but it just stroke me as a bigger cognitive leap)
3. using different pattern than dices on e.g 3 . May be less relevant for small kids that have not seen dices before, but I think there will be a reinforcement/recognition factor her.
I dont know much about the theory and behind this, but I sketched up my own basic pattern fixing the two last issues here:
https://drive.google.com/a/newschool.me/file/d/0B8CItqQhTUNlZjhGWjVGVlhyajQ/view?usp=sharing
This guy seems to be an one of the experts http://udenver.academia.edu/DouglasClements
Would be interesting to hear other opinions on this issue.
I am really late to this conversation and no one may ever read it. But I think the two different arrangements for 7 are wonderful. Within the circle the 7 dots are obvious because you can easily see the 6 and then the 1 extra to the side. I see the 7 circles arranged as a set of 5 and a set of 2. 7’s are hard for students to master. But if they think of them as 5 groups and 2 groups and add the partial products together, they can solve the fact. So if you look at the 7 groups of 7 card. 5 sevens is 35 and 2 sevens is 14, so 35 + 14 is 49.
I’ve used similar cards found here! http://teachmath.openschoolnetwork.ca/wp-content/uploads/grade3/documents/multvisrepcards.pdf
These array cards are also great because of the way the dark lines show up. It helps them see, for example, 8×5 can be thought of as 5×5 + 3×5.
https://777d6de7-a-62cb3a1a-s-sites.googlegroups.com/site/get2mathk5/home/math-toolkit/sequencing-numbers/ff-mutiplication-division/arraymultiplicationflashcards.pdf?attachauth=ANoY7crUHGzXdmRpNaDbUTrlIeIMr18oIagIUgAVwYP7GMmiU5HVtR6EAwddSlXlZ-w7HWZFG-hNbO9zZJh2pLqsguaDWCwpvKsvtkRbzCG6PXph13pDMSQ-wgq1D5OeABNVMrjy5hhdkgsA6kevOlEdTN_MRZUAOw2l3IudR9BdsgE0Ii30bZjT8H7o-p7NxNOlgBkzq4Woy0QMjdCXrUKnXZERs-bhX0RDK9pjkKAb3OncB3C1M4-7pk0PUuO_6jwJSivkx-TyIyyYKWaLPb-HON0tYIjawKV8_Is40fxJJEJsmKwv0dP4aSkzBchrJqaBhJKDVyEzQfzwdf54Xv9iAPkuz6OSmQ%3D%3D&attredirects=1
Thanks for sharing the cards Ashley. They’re a nice little addition!
Love this! I plan to try them with my 5th graders who are struggling with math fact memorization. The picture in the middle of the page says 3 X 6 = 30. What am I missing? Is that supposed to be a mistake or…
I tried using the cards with a fifth grader last week, hoping that they would help her develop her multiplication fluency. Well, what I discovered was that she had a hard time subitizing even 1 group of numbers, let alone multiple groups in the circles. She had to keep counting them on each card.
When asked, she said she had never used such cards, so I took this to mean she had never been exposed to subitizing with addition or subtraction. It really never occurred to me that she wouldn’t recognize 7 dots. So next week, we will be working on just the lower numbers and then build up from there. This is a great reminder to me to continually search for gaps in understanding. Thanks so much for these cards!
It’s amazing what gaps we find in student thinking when we start digging! Nice work Marian and thanks for sharing!
Can’t wait to use these cards with my students working on developing multiplicative thinking! Thanks Graham!
Love that you’re always seeking ways to engage your students Andrew. Self-contained isn’t the easiest of teaching positions but definitely one of the most rewarding! Can’t wait to hear how it goes when you give them a try. I’ll be looking for a post over at https://thelearningkaleidoscope.wordpress.com/
Cheers!
Subitizing activities are an integral part of the development of all facets of number sense. Some kids do not develop this mental capacity as automatically as some others and these activities are such a wonderful method to get those kids caught up, or in your case to begin the process of developing multiplicative reasoning. Thanks for sharing.
Absolutely!!! I think as teachers we all get the “big ideas” but it’s identifying the ways to bridge the learning in-between that we sometimes find difficult!
Hopefully this piece of the puzzle will help pick up a couple more students.
Thanks for checking in Steven and for the comment.