It’s never been a secret that Superman fears Kryptonite. But I think the same can be said for many 2nd grade teachers and the way they feel about teaching money.
There’s no way around it…teaching money to students is hard. With money comes a level of abstraction that’s really difficult for students to wrap their heads around.
How can a dime be worth more than a nickel if it’s smaller?
We knew the road ahead was bumpy, but we moved forward nonetheless. Only this time we decided to tackle money with some base-ten understanding up our sleeve.
We started with a quick brainstorming session:

Students identified coins and equivalent value combinations.
Then students were given a Hundreds Grid and asked to create “money” that represented the combinations they identified. We hoped that by connecting money back to base-ten, future student thinking would be grounded in conceptual understanding.

The value of a quarter made with 2 tens (dimes) and a 5 (nickel).
Lots of mess taking place but also lots of concrete understanding…

Some students wrote the value of coins on the paper without prompting…we liked this!

The fruits of our labor.
After students had finished constructing the manipulative, we had them explore and model combinations for different values. How many different way can you represent 30 cents? 35 cents? 40 cents?
Knowing the paper base ten money wouldn’t stand a chance during the game, the wooden base ten blocks were introduced with coins and the connections continued.

How many ways can we represent the value of a quarter?
Note: in the past I’ve introduced the wooden blocks without having students create and design the paper money upfront. Having students create the money was a new wrinkle in the lesson. Our hope was that students would make a conceptual connection when decomposing money in the game.
As students explored the money they were able to make the connection and see how 4 quarters was equivalent to a dollar. (4 x 25 = 100)
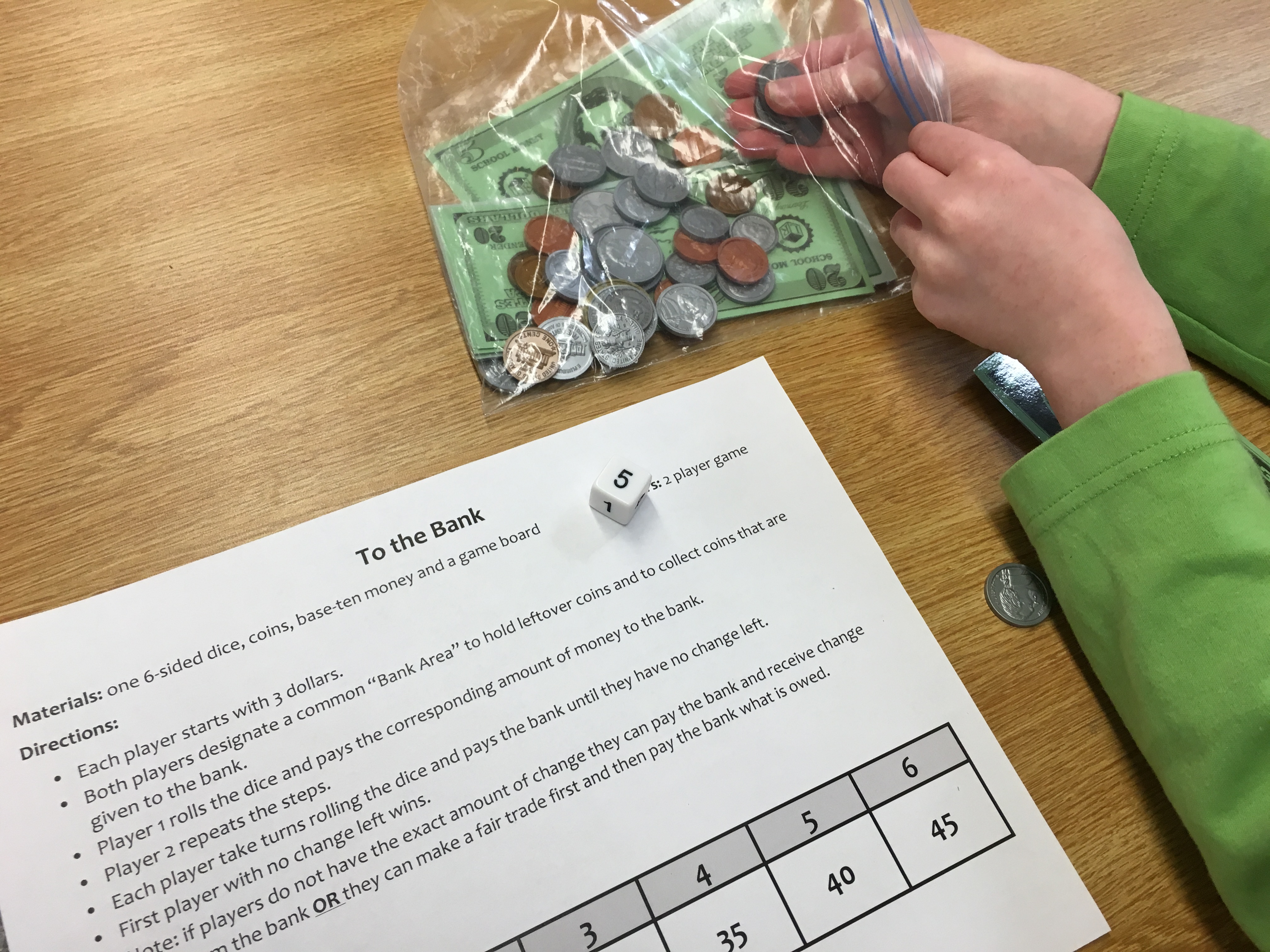
Once their notice and wonders were fed it was time to build fluency through conceptual understanding. So we played “To the Bank“…

Two students came to the carpet and the class created a fishbowl as they modeled the game. From the onset, each student started with 4 quarters. Player 1 rolled a 4 and needed to pay 15 cents to the bank.
Player 1: Mr. Fletcher I can’t go.
Me: Why not?
Player 1: I don’t have 15 cents to pay the bank. (Sitting with 4 quarters in his hand)
Me: Well then I guess the game is over. You lose. (player 1 sits stunned on the carpet)
Player 2: Mr. Fletcher, he has 15 cents but he can’t pay for it with a quarter. He has to break apart the quarter to pay the bank.
Me: How can he do that? I don’t have extra money laying around.
Player 1: But he bank does! Can I give the bank this 25 and they give me back 2 tens and a five?
Bingo! He modeled the fair trade, paid the bank, and they played through a couple more rolls and the class was free to play.
Receiving change is almost as abstract as money itself. Because I’ve failed numerous times when tackling money I’ve come to find that having students explicitly conduct a “fair trade” before paying the bank works really well.

This seems like a lot of steps and to be completely honest it is!!! But as students begin to construct their own understanding these steps are really important for students to internalize themselves. Physically acting out the fair trade and talking through the steps helps students make the transition from concrete to abstract. There’s a lot of math happening here and students need to see it.
It’s NOT efficient to have students work through this fair trade every time and thankfully, as time passed a couple of students began to find shortcuts. Not every student in the class needed to preform a fair trade to pay the bank but the majority did and that’s ok.
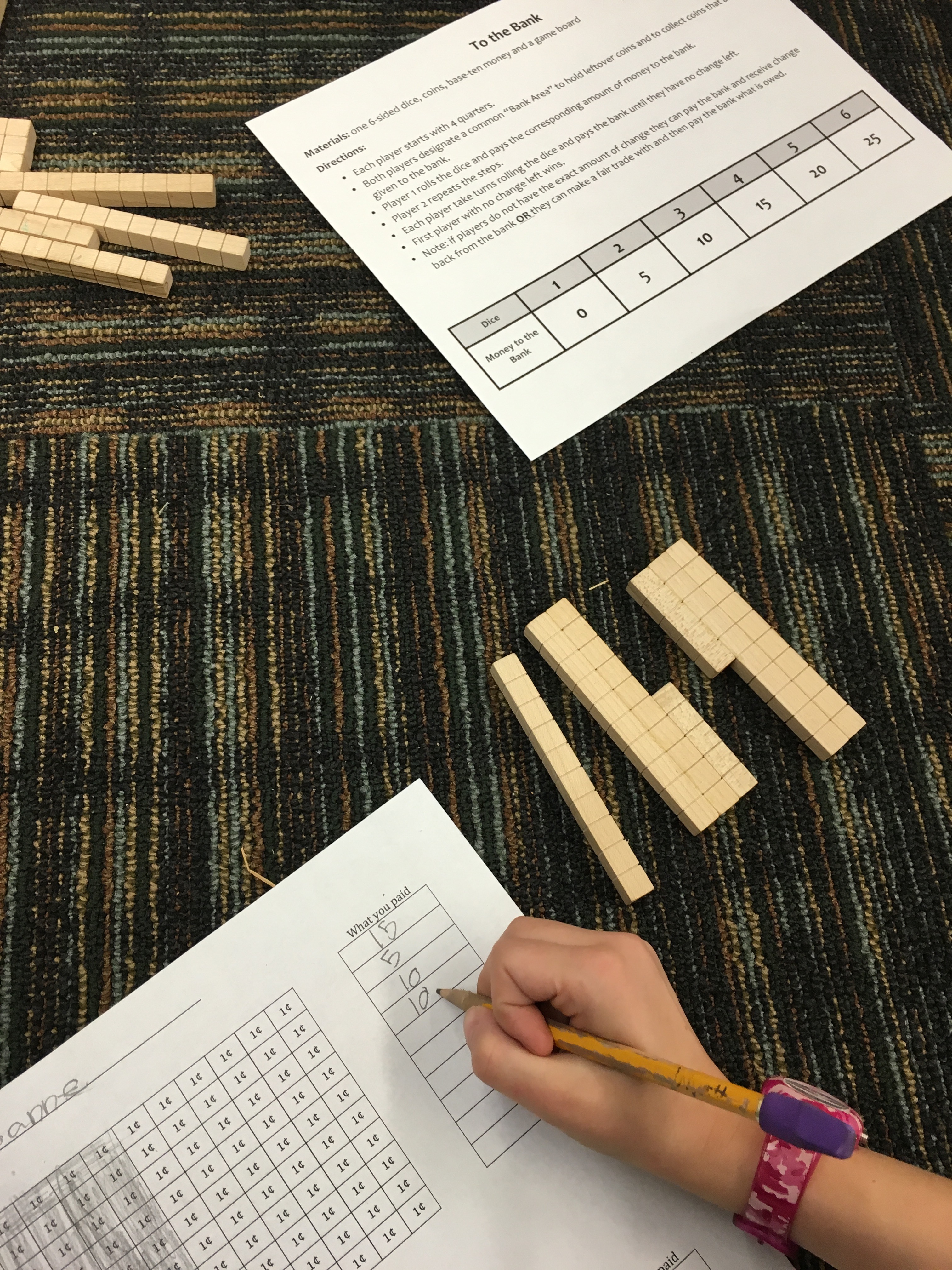
As an option, some students recorded what they spent and modeled it on a hundreds chart.

First player with no money left over won the game.
By the end of class there were 4 students that moved from base ten money to actual coins which was great to see.
Next time we play To the Bank with this class we’re going to start with coins only. As students are playing we’ll reintroduce the blocks to those students that still have a difficult time understanding the fair trade/making change idea.
There was an alternative board that was introduced to a handful of players. The board had greater amounts of money owed and students started with three $1 bills instead of 4 quarters.
All in all, it was a successful 75 minutes spent in 2nd grade and money isn’t feeling so scary around these parts. We still have our work cut out for us but the math residue has been laid and we’ll take that understanding to the bank!
We’re just hoping the bank doesn’t get robbed before we return to the game.
Side note: Even if you don’t have wooden base ten blocks you can create money. Foam base ten blocks work as a nice alternative after some handy scissor work.

Base ten money made from a foam 100.

Hi Grahman
I am in Australia and I always check in with your website as part of my research for conceptual understanding and connecting the big ideas. We of course have a 5c, 10c, 20c, 50c, $1 coin and $2 coin, with our $2 coin being smaller than all bar the 5c, and the $1 smaller than the 20c & 50c …so have been thinking about how to convert your thinking about value of money and think I’ll go with the $1coin – although it means more one hundred charts – it will help with the link to decimals too. I like the idea of trading a larger value coin for equivilent of smaller coins, and the game is perfect for checking in with where my students are at with their understanding of this (they are a higher grade with a range of abilities).
Cheers
Awesome. Foam base ten blocks are cut and ready to go. I am heading into 2nd grade classrooms and explore money. Thanks!
*to explore money
Okay, so I’m doing this on Monday for a video lesson thing I have to do. I’m doing the cutting of the hundred grids on Friday and then they are going to use the manipulatives to do your To the Bank second grade 3 act task on Monday. Excited!!!!
I really like what you’ve done here. The step you added by having the students cut the hundreds grid apart is a great way to help the kids connect to the base-10 blocks. I also like how kids have options for the tools they want to use, and how you’ve differentiated the game for kids ready to move on. Will be sharing this with our grade 2 teachers. Thanks!
Cheers Joe…You inspired the use of scissors for sure. By giving students less up front, they had more opportunity to unpack their understanding. The power of scissors is undeniable. I might need to start calling you the “Sultan of Shears”.
Wonderful post, G-money.
Would a razor blade or exact-o knife work on cutting those foam blocks?
Thanks Andrew. I actually used scissors to cut the base ten blocks…but I assume a knife would do the trick as well.
Great, Graham! Nice ways to make wrinkles in understanding money!
Cheers Simon! I was going to do one for the Euro but who knows if it will be around in a couple of years.
I think it must be harder because the dime and quarter are just called by their value. More to learn than for us.
… well, in fact, we don’t have quarters. That’s quite nice mathematically, to have a 25.
Those are all great points Simon! Our 25 piece screws everything up with base 10. It would be nice to call them a 10 cent and 5 cent piece.