First week back to school and I was chomping at the bit to begin working on my #1TMCthing.

My quick backstory about Vertical-Non-Permanent-Surfaces (aka VNPS)

• I first found out about VNPS on Nathan Kraft’s blog
• which referred me to Alex Overwijk’s Blog
• who shared that Peter Liljedahl is responsible for bringing VNPS to the forefront
• I attended Alex’s #TMC15 session about VNPS and he got me all fired up

In Georgia, 5th grade students start the year with order of operations. Easy right?  Not so fast!  PEMDAS has been the death of conceptual thinking for years.  That’s why I refer to it as Please Excuse My Dumb “A”  Strategy.  If you follow Fawn, you know what the “A” stands for.  In a nutshell, the context should dictate the order of operations…not the rule.

We started here with It All Adds Up:

What do you notice (WDYN) & What do you wonder (WDYW)

Our main question: What types of coins made the $1.00 and how many of each coin?

Students brainstormed for a little bit and came up with the information they needed to solve the main question.

types of coins in the bank                  total number of coins in the bank

To begin, students were given this 3-Act Recording Sheet and some tools.

Some groups were given a handful of coins to manipulate their thinking.

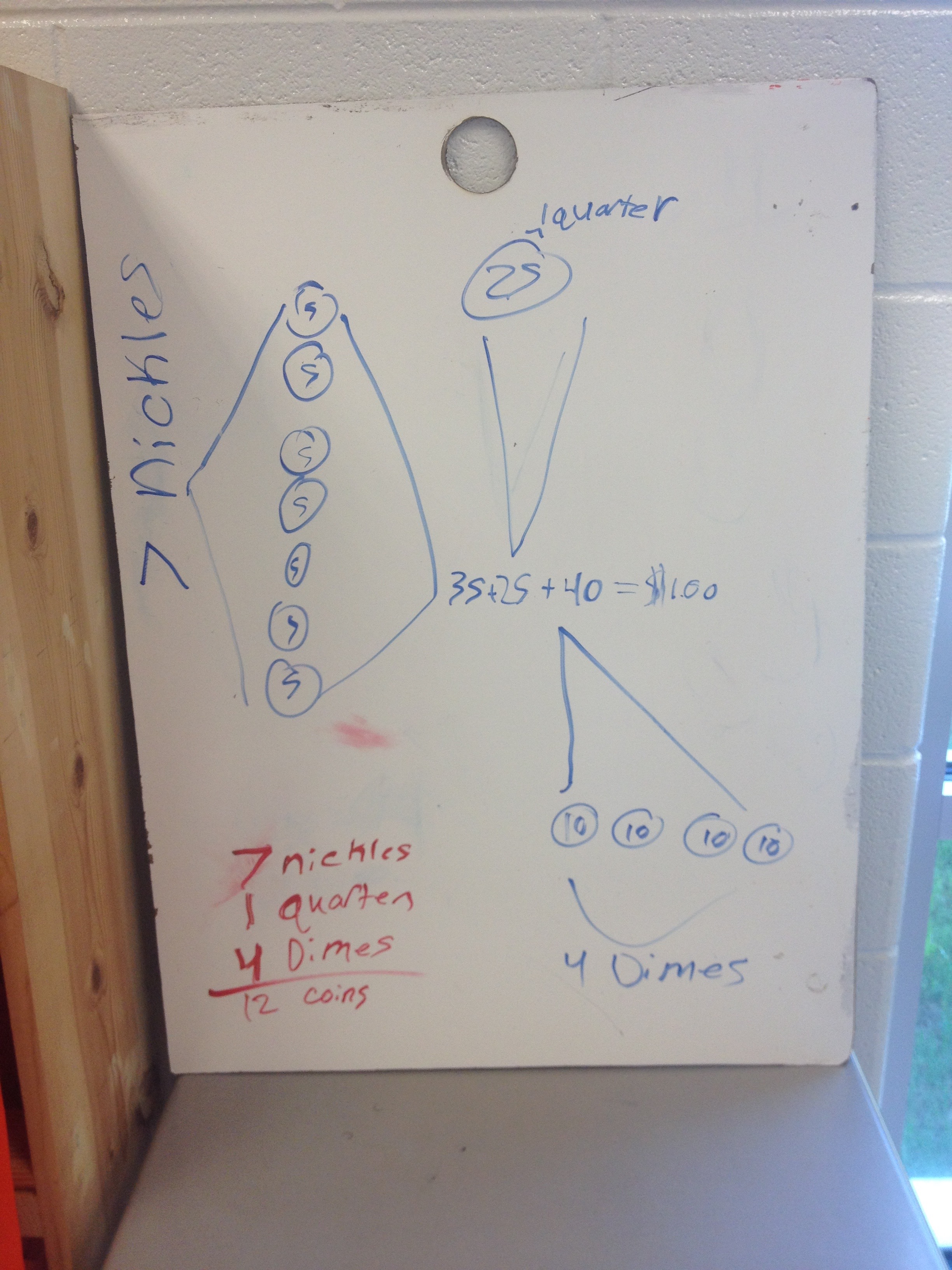
The process that students underwent as they tackled the problem was great to watch.  I didn’t need to facilitate the conversation.  Students started by eliminating the pennies based on the information from Act-2.  They counted out 12 coins and began adding them to make $1.00.

I heard lots of “what if we…” and “let’s change the ___ to a ___”.  The use of coins made the combinations more accessible to students and they were much more willing to engage and dive in.  The end result…

As groups worked through the problem, they recorded their thinking on the Vertical-Non-Permanent-Surface.

To differentiate, two groups were given wooden base-ten blocks cut in the denominations of money and asked to create a dollar (flat = $1).

They realized they had represented 13 coins and they needed 12. The 2 tens and one 5 are glued together to make one quarter.

We were getting close to wrapping up the lesson and every group used the traditional algorithm to prove their work… except one.  Using the VNPS allowed us to direct the rooms’ attention to one particular board.  We shared this board as an example for how we can record our thinking using an expression.  The difference between expression and equation is a beast in itself… but that’s for another post.

1 x 25 + 7 x 5 + 4 x 10 = 100
Is this expression (using 2 lines) mathematically correct?

I asked some students why the answer wasn’t 1640 (working left to right using no order of operations).

• Me: Why is it not 1640?
• Student 1: Because you need to multiply first.
• Me: But I thought you needed to start left, then move right, and do them in order. Now I’m confused.
• Student 1: You need to multiple first or your number will get bigger than a dollar.
• Student 2: Yeah. Like you’d have $16.40 and that’s not what’s in the bank.  We know it’s a dollar in there.
• Me: Hmmm?  OK.  So do you always multiply first before adding?
• Student 1: I’m not sure.
• Students 2: No just when you’re doing this problem.
• Student 1: But you could also multiply first for other problems too I guess…it depends on the problem.

Music to my ears.  The context should drive the order of operations.  In the end, the class watched Act-3 and high-fives occurred all around!

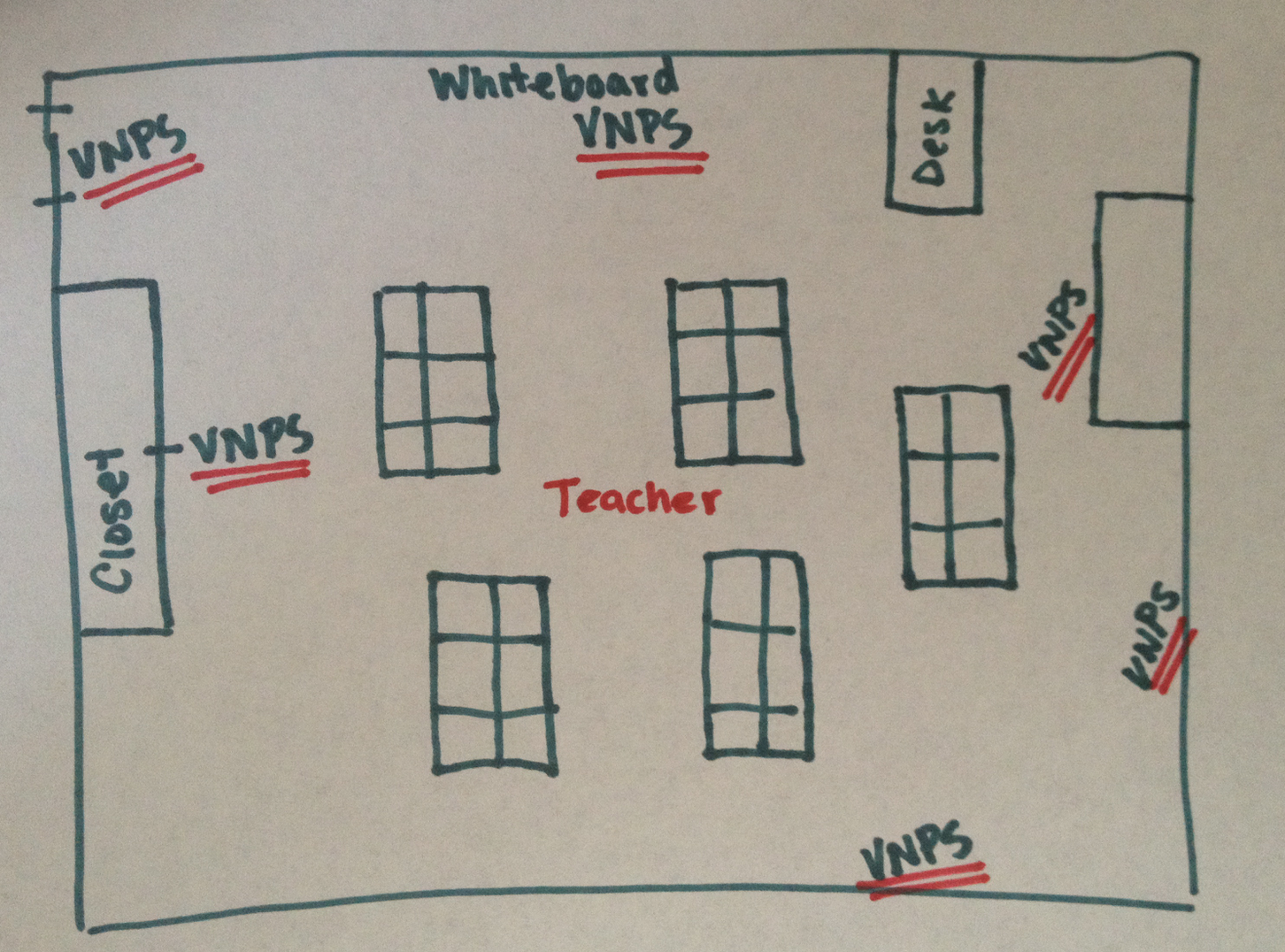
How we implemented VNPS:

• I went to Lowe’s and purchased a large shower board.  They cut them into four 2ft x 4ft sections for me.  Got home and used a circle saw to cut the hole.  I recommend using a big hole so that they can be easily transported by using a single strap.
• We attached them to the wall using Command Hooks. 
• We hung hooks all over the room (on cabinets, closets, metal grate for A/C, the classroom door).
  

  Where you see VNPS is where students had a whiteboard.

My takeaways:

• It’s these types of ideas that are shared at TwitterMathCamp that make it a worthwhile conference for EVERY TEACHER (regardless of grade).  Vertical-Non-Permanent-Surfaces should find their way into every classroom.  There is not a kid I know that doesn’t like writing with an Expo Marker on a board.  As elementary school teachers, it’s time we leverage this love for the Expo.
• VNPS are amazing.  As the teacher, we were able to stand in the middle of the class and monitor the work of each group.
• In terms of assessment and scaffolding the learning, we were easily able to identify the order of sharing student work during the closing (a la Peg Smith).
• The context should always dictate the order of operations.  Not Please Excuse My Dumb A_ _ Strategy.
• Throughout the lesson, students never asked if they were right.  They kept going back to the information given in Act -2 and verifying if their model matched the identified variables (12 coins composed of quarters, nickels and dimes). <—–WINNER

Sidenote: Andrew Gael has a great write-up using this task with his special ed students. He owns differentiation at a level I strive for and is someone I lean on heavily when it comes to reaching every student.

Without Nathan, Alex and Peter I never would have been introduced to VNPS.  Thanks gentlemen!