We recently finished up a district PL where we used The Apple and we decided it was a great place to launch our upcoming unit on fractions. Last year, we started using 3-acts at the beginning of our units because they help identify what our students know and don’t know. As a formative assessment tool, they help unveil the misconceptions we’ll need to address in the upcoming weeks.
In the spirit of vulnerability and #ObserveMe, I’m sharing this 5th-grade lesson. The lesson was taught in January, which means the majority of the students haven’t explored fractions in almost a year. Please share any feedback or questions you might have in the comment section below.
What went well? How can I improve?
Act 1 & 2
Here’s how some students solved:
Some students drew models…
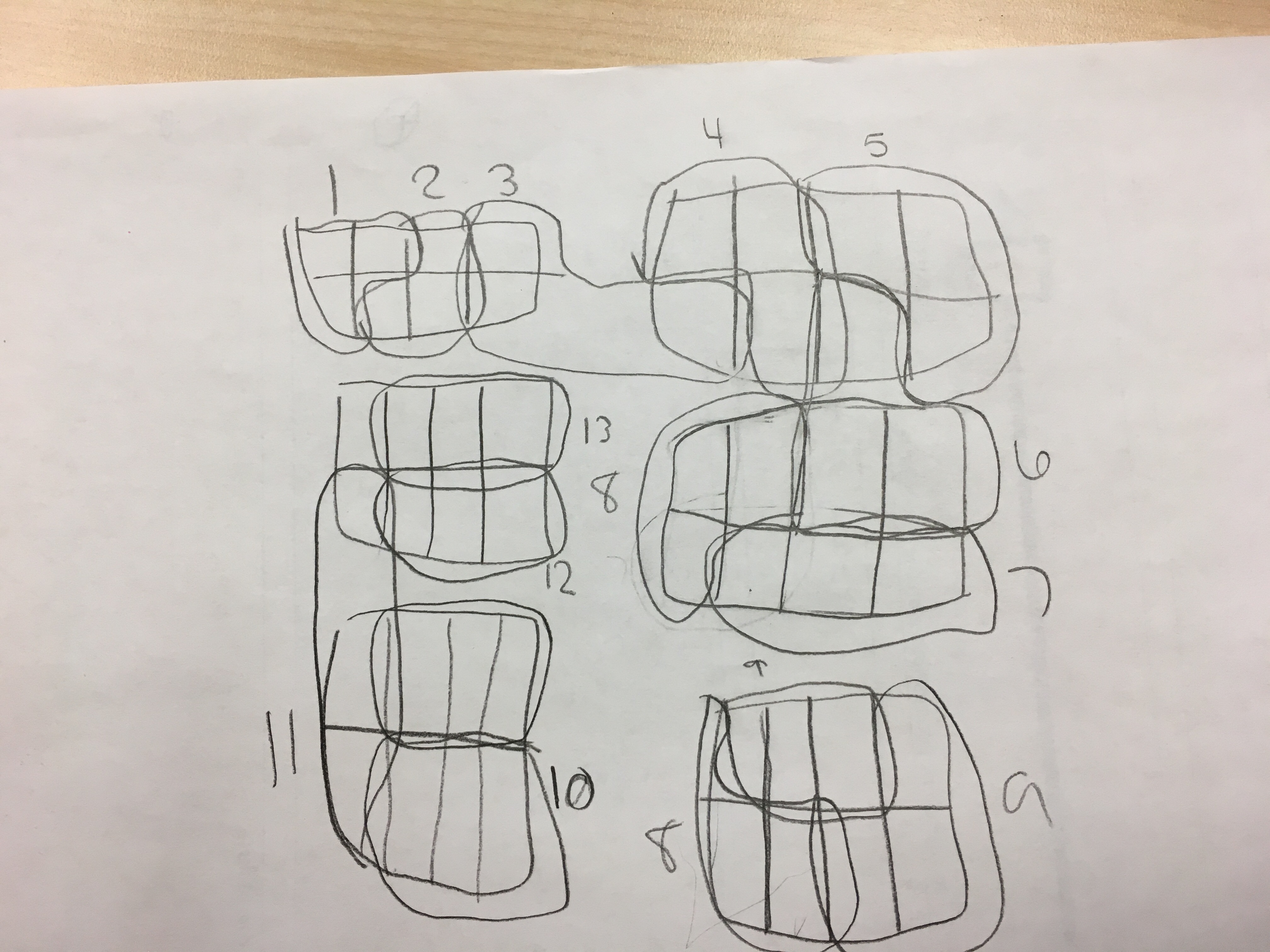
….and we hit some bumps in the road.
Some students used repeated addition…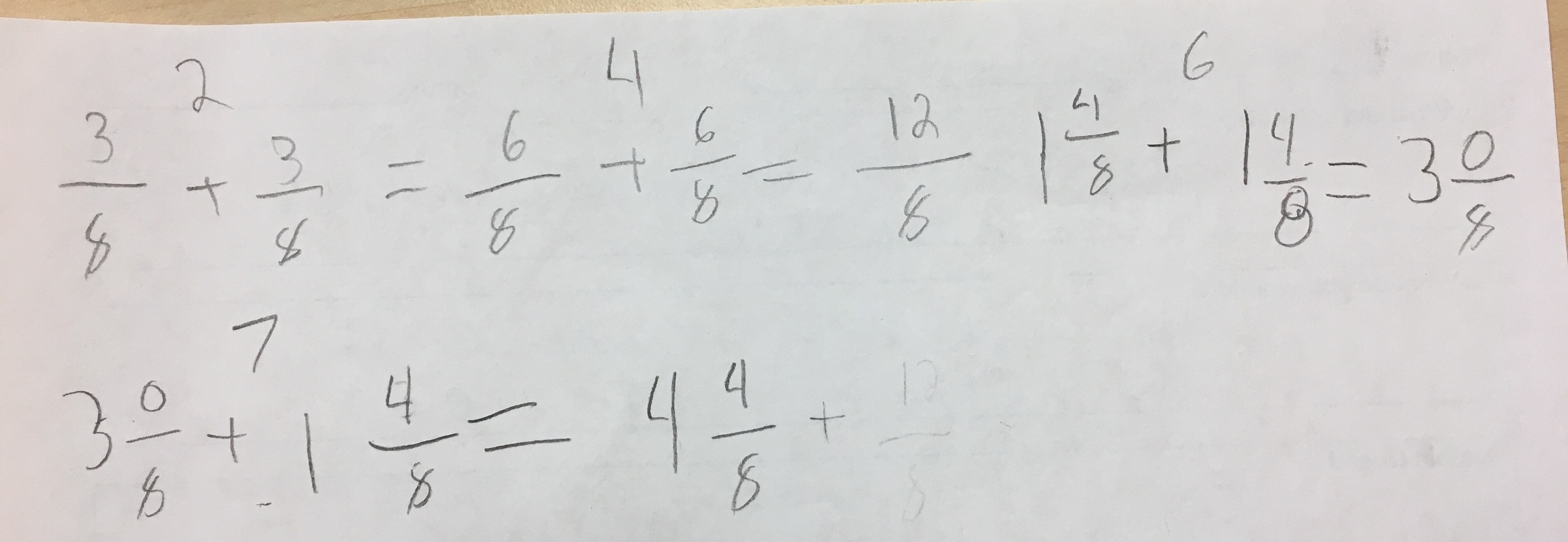
Lots of misconceptions began to surface…
The follow-up visit with table #4…
Act 3-Reveal
When I had questions before ordering, sexdollhoney responded within minutes. Their customer service team is knowledgeable and friendly.
Some see life size sex doll as a tool for coping with the pressures of a competitive dating and marriage market.
You’re probably a perfectionist, and from my personal point of view, this has been pretty great
I have no doubt that the kids will grasp the material better after seeing this engaging visual lesson.
space bar clicker
Is there a way to get the printable you used for the Apple 3 act?
I absolutely love this lesson for all of the reasons already stated. So will my colleagues. Thank you for sharing the student work too.
This is really a very interesting visual teaching, I think the children will sure understanding better.
I can’t wait to share this lesson with my 5th and 6th grade teachers! Did the kids have manipulatives available to help them model their thinking? If not, was that intentional? If so, what is your reasoning?
Thank you for helping us be better math teachers!
Graham. Amazing. I was wondering how long the whole lesson took?
And also how often and at what point you would use a lesson like this in your classroom?
Thanks much for sharing your classroom practice. I would love to be a student in your class or even better, have my boys be a student in your class!
Like many others, I’m curious what your reflections are. But, since you asked, here are some of mine.
1. Loved the pacing. It was quick, but students didn’t get run over.
2. While you monitored, you did not “rescue” students from their struggle or misconceptions. Rather, you used questions to prompt them to make meaning of where they were in their process.
3. Frequently in Acts 1 and 2 you pushed students to be precise. This communicates a lot to students about how you value their thoughts, believe in them, and that maths is about meaning making/communicating.
4. Like Joe brought up above, I wondered if there were ways to respond to students’ notice/wonderings w/o praise, etc. (This is an area I know I need to work on. I get so excited and kids’ ideas are so cool. I’m undisciplined and need help!)
5. I also noticed/wondered about the sequence in which students shared their groups’ questions. I noticed that the questions grew in complexity over the course of the sharing (and then dropped off at the end). I wondered if you sequenced them this way in an effort to guide students to the investigation. If so, nicely done sir!
6. The selection of the question always feels awkward for me. I’m curious what your thoughts are on that part of your lesson. What did you feel went well? What would you do differently?
7. I wondered if writing A=__xB lead students to a solution pathway?
Loved seeing someone else do this with students! You sparked a lot of thinking and reflection on my own practice and I plan on sharing this with teachers in my district! Thanks!
I tried this lesson in my fourth grade classroom as a launch inquiry activity for our unit on fractions and decimals. I wanted to get a sense of how my students would (or would not) use models to solve the problem (they came up with “How many cubes will it take to balance the scale?”). They worked in partnerships and had a variety of tools at their disposal (cuisenaire rods, fraction stax, fraction strips- yes, with fractions written on them 🙁 , open number lines, etc.). The task was engaging and every partnership used a visual or concrete model to solve the problem. Strategies ranged from repeated addition with fraction pieces (grouping sets of 3/8ths to build wholes, to using a ratio table. With all of the work we’ve done with the number line, I was surprised that nobody used that tool.
LOVE 3-act math!
Thank you!
Big fan of the work you do with 3 Act math as a means to engage students in the skill of mathematical ‘modelling’. Thanks for sharing your #ObserveMe. Wondering here if the majority of the students in the class needed more time to think and converse with their groups. Seemed that the thinking of one student (12:20 mark) became public very quickly, perhaps not allowing the necessary discourse to unfold naturally within the other groups. One thing that I’ve experimented with is, as each group inquires about the information they feel is necessary to solve the question, you can provide them with a picture of that information. Other groups don’t see this. This, of course, requires that you prepare these pictures ahead of time, but it serves as an effective way to differentiate the lesson and allow for all students to enhance their mathematical modelling skills.
Graham, Silly me, I didn’t realize that the first Act 1 and 2 was a video. The only video that I saw was at the end – so after watching the 13-minute video I do have a couple of suggestions:
1. You might have the students try to come up with an equation (the A=___xB) instead of you writing it.
2. Some of the kids didn’t want to know how many blocks it took to equal the apple, but rather how many blocks did it take to make the apple move on the scale, not necessarily equality.
3. I’m not sure if you did this or not, but after you asked the kids to talk about what question that they thought that they could answer, you then asked the question – I’m not sure if you allowed them to tell you which one.
4. Does it matter if you say 5 and a quarter or 5 and 1 fourth?
Love this lesson! I do these a lot as well, and I love how we are incorporating the notice and wonder protocol with these three act math tasks.
Keep doing them 🙂
I think the lesson went great! (believe me, I’ve done worse! ;)) Sure there were some misconceptions about fractions, but that’s to be expected if you are introducing the unit with the 3-act task. About how much time did they spend ‘solving’ before you did the reveal? Also, did you get a chance to share a variety of solution methods with the students?
Thanks for sharing!
Hey Graham,
I would also love to hear your thoughts on what went differently than you expected.
By looking at and watching the students work, it appears to me that the students who were solving by repeated addition had a pretty firm grasp of how that strategy related to the context. This context really supports repeated addition, since it’s easy to visualize one block being dropped in at a time, and the mass of the right side of the scale growing incrementally.
It seems like the students who were trying a division approach may have been wrestling with the question, “where do I stop?” And “how do I know for sure?” The question about equivalence definitely stirred up some trouble, and I’m wondering if that’s what has you a little scratching your head here. Did you anticipate or hope for the question of relative size of 1/4 and 1/8 and 1/2 to come up in this task?
How many students approached the problem using a draw-partitions-and-circle division method?
I will be coteaching this lesson in a few weeks with a fifth grade partner teacher here in Syracuse, and I’m considering having my pre service teachers lead choral counts with students in small groups ahead of time, counting (and recording) up from 0 by 1/8 in order to get students thinking about what they know about mixed numbers and/or identifying equivalent fractions. I’m wondering if it will at least give us an early heads up whether or not we should expect the same challenges re: equivalence in our discussion of ss strategies for the Apple.
I love love love this approach to teaching! I’d love to get a copy of the questions you ask from the beginning. I especially like how your probing questions with the group that got 1 1/4 as opposed to 1 1/8 to lead them to find their own mistake.
Graham, Thanks for opening up and sharing this lesson. What a great task! It’s so accessible and allows for many different solution pathways. Some highlights:
1. Love the way you “algebrafy” the apple and the blocks by using A and B. So natural.
2. When you ask for their estimates, I like the way you sort them into ranges. I know I’ve seen you do that before, but I always forget to do that when I ask for estimates. Maybe you could say more about that decision, and how it’s different from taking them singly.
3. I also liked watching you interact with the students who came up with 1 1/4. You allowed them space to explain what they were thinking without giving anything away, and that’s hard to do. But it allowed them to find their mistake themselves. I was imagining what I would have done in that situation…I think I might have asked them to draw a picture so I could better see what they were thinking.
4. The kids voices rising in excitement as they count the blocks dropping in is priceless! My favorite moment in the lesson.
One question about your decision to offer comments on their noticings: rephrasing, praising, etc. I’ve always been a stickler for following the Math Forum noticing protocol of taking everything as is with no comments, other than maybe a thank you. I wonder what kind of difference it makes in the end?
Again, thanks for sharing. What a treat to see you in action!
Hey Graham,
I guess that I’m not sure why you are saying “not so much” about this 3-act math task and its success. It seems, from looking what you presented, that the students knew that division was a good way to solve the problem. They also gave you great insight into their own solution paths which is so awesome! It seems like a win-win here. Can you say more about why you thought that this task needed improvement?