As elementary teachers, we rarely have the opportunity to explore division of a fraction by a fraction. When we do, it’s normally accompanied with Keep-Change-Flip or the saying “Yours is not the reason why, just invert and multiply.”
Both are conceptual cripplers.
I’ve been drafting the 4th installment of the Making Sense Series involving fractions and I’m sharing this post as more of a personal reference should K-C-F make its way round these parts again…and I’m sure it will.
Side note: A while back Fawn and Christopher each shared a post about division of fractions using common denominators. Both posts left lots of math residue and are well worth your time.
Let’s start with a model for 3/5 ÷ 1/4.
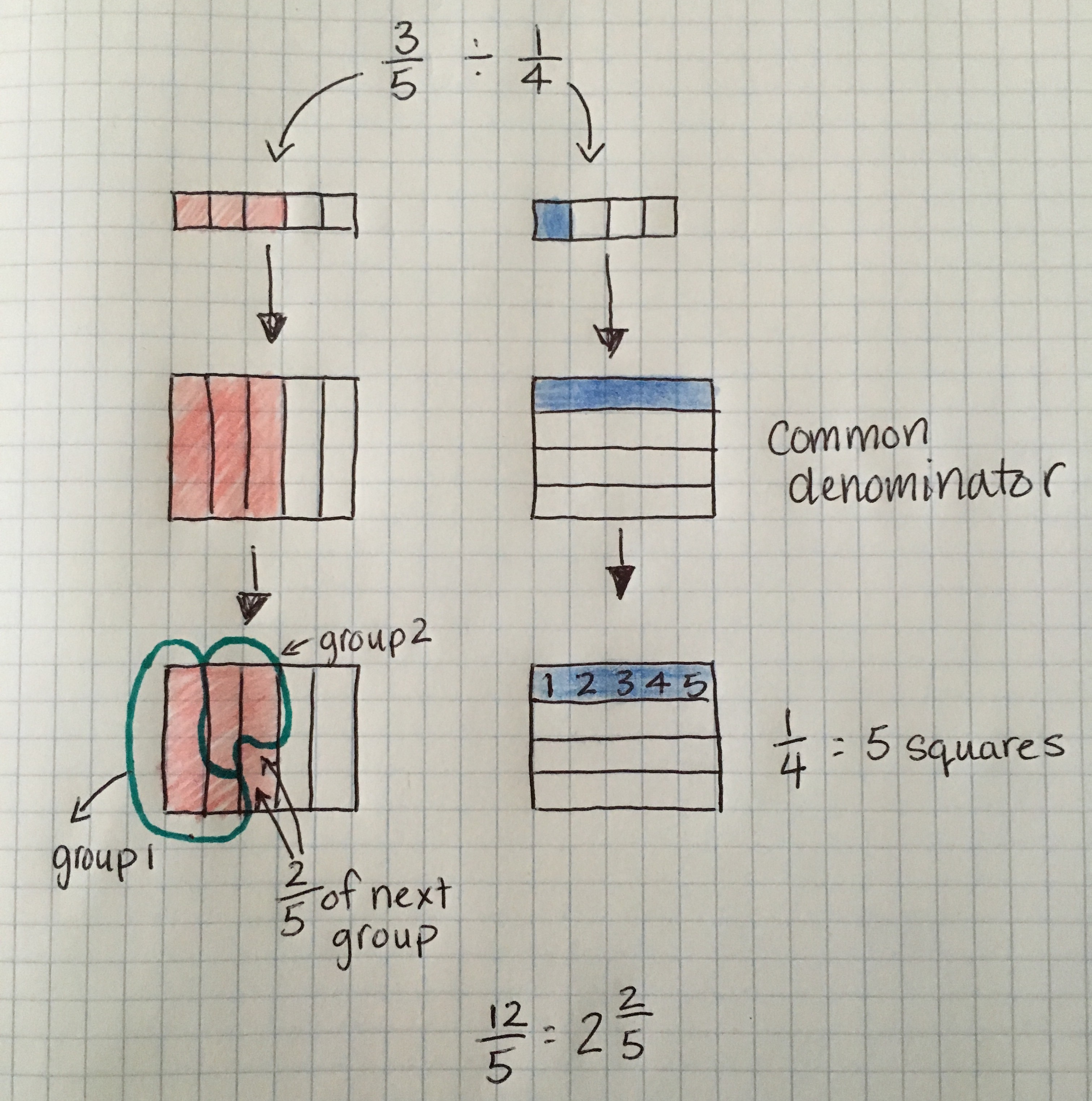
Modeling measurement division of fraction by a fraction.
At some point along the way it becomes inefficient for students to draw models once the conceptual understanding is established. As students represent measurement division of fractions they should be formally recording their thinking.
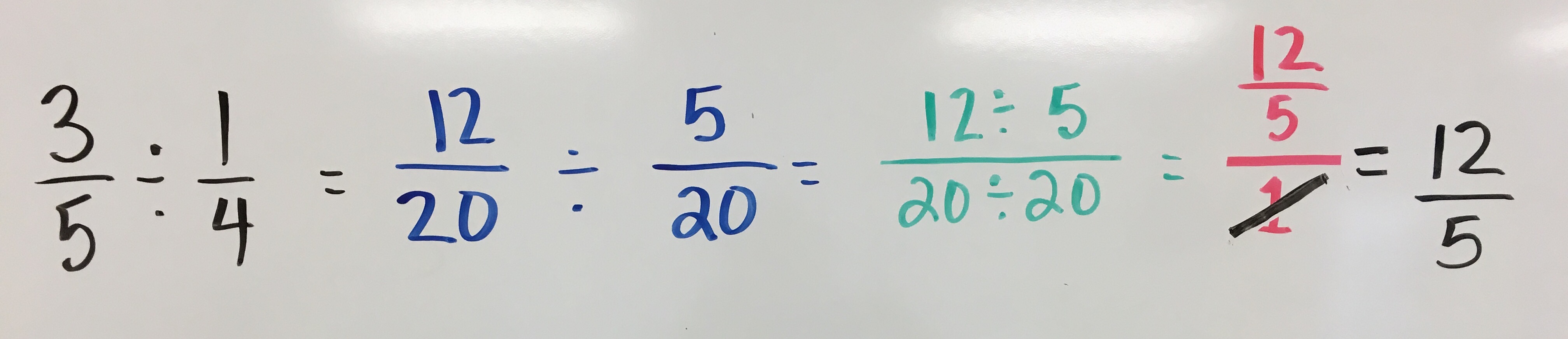
From here students generate their own algorithm (shortcut). They begin to recognize that they will always get a denominator of “1 whole” so they begin to purposefully leave it out. In doing so, they become more efficient in the procedure of dividing fractions.
Some students begin to eliminate the green and red steps from the above equation because they’re seen as repetitive. We’ve even had one student that “invented” and generalized cross multiplication for division of fractions as they searched for ways to record fewer numbers and symbols.
It looked something like this…
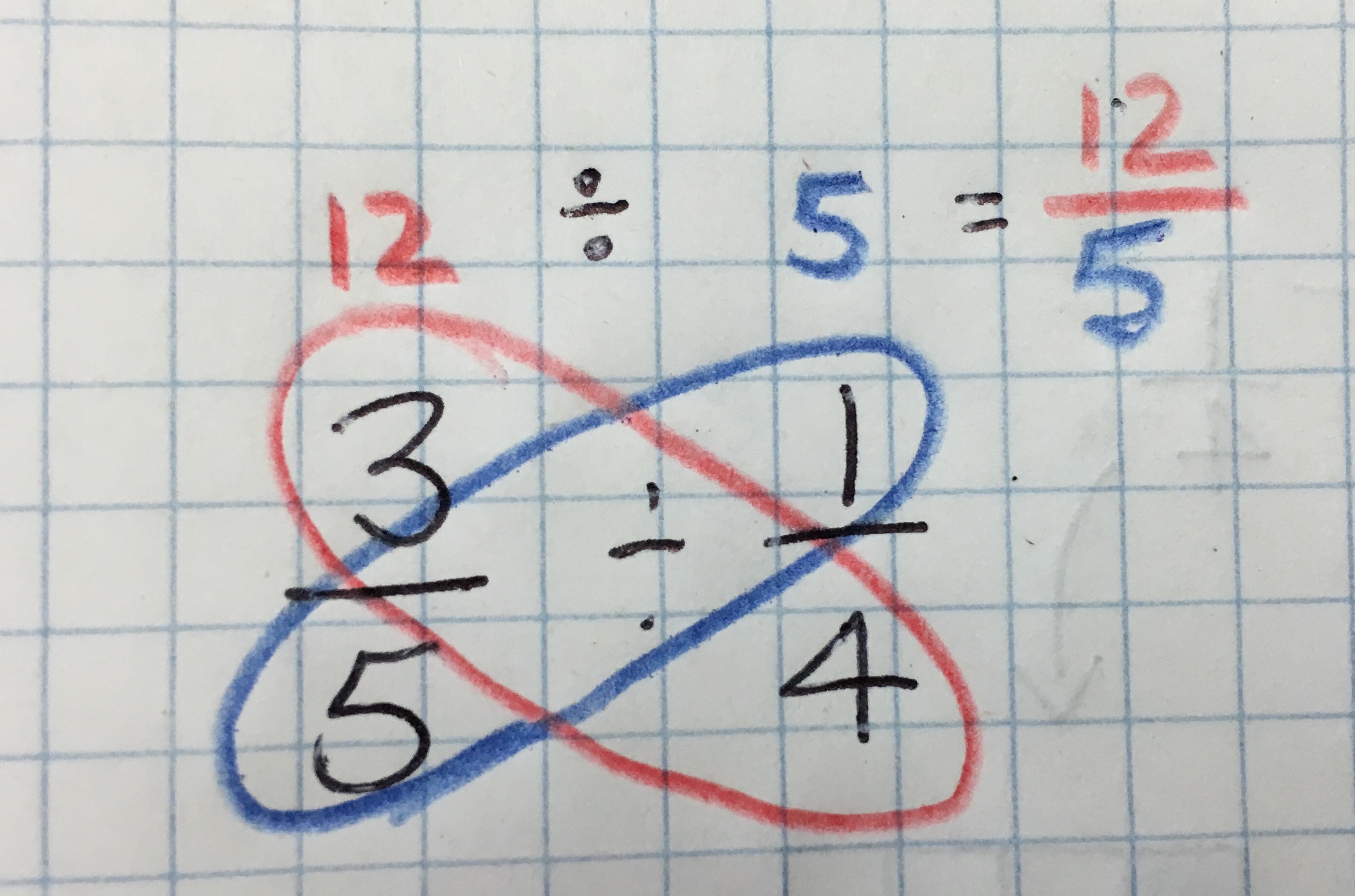
NOT A STARTING POINT!
I keep reminding myself that if fractions are the gatekeeper to algebraic reasoning then I need to slow the process down and conceptually understand what’s happening. This includes K-C-F.
As students understand the power of creating a whole number denominator they begin to search for more efficient ways to get 1 whole. It’s here that they being to explore with equivalent fraction and the idea of using the reciprocal to create a whole.
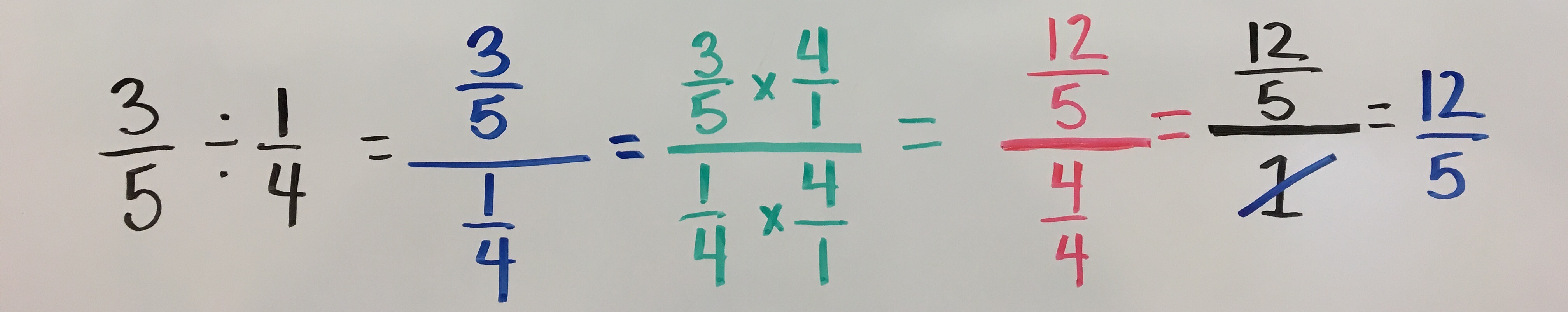
What I’ve realized is that aside from complex fractions, the underpinnings of this equation are developed in the elementary grades.
- 5.NF.3 Interpret a fraction as division of the numerator by the denominator (a÷b = a/b).
- 4.NF.1-Explain why a fraction a/b is equivalent to a fraction (n x a)/(n x b).
- 3.NF.3.c- Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers.
Just like before, students will look to generalize the equation above and find shortcuts. They’ll do so by eliminating repetitive steps which would leave them with…
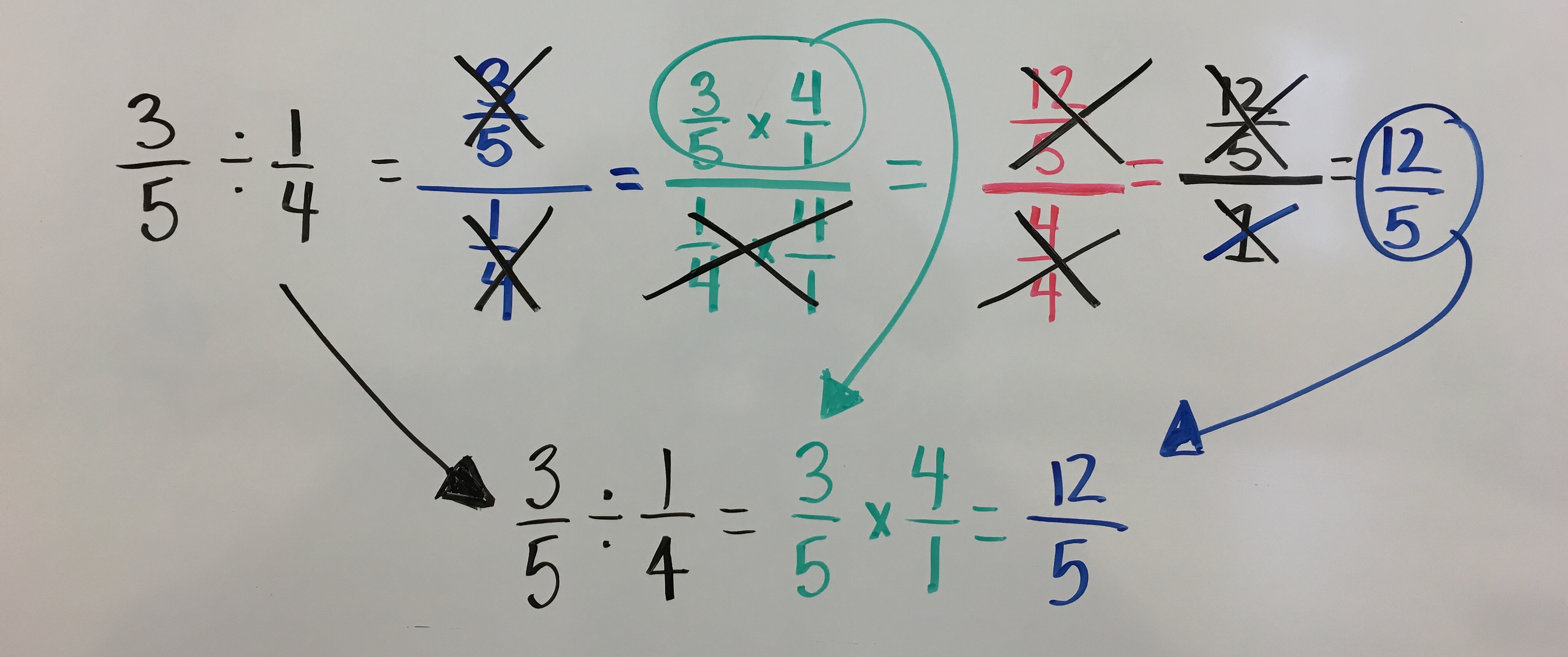
Invert and multiply.

In measurements, fractions appear whenever units are not small enough to express quantities in integers. For example, five quarter-dollars will buy you exactly as mush as a dollar and a quarter. One and a half dollar stands for exactly the same quantity as three half-dollars or six quarter-dollars.
Fractions are unavoidable and sooner or later we all have to learn to work with fractions. The mathematical usage of the word fraction has a very clear everyday connotation as a part of a bigger object. It would be unthinkable nowadays to just introduce fractions as a pair of numbers and postulate their basic properties. Still, to express fractions one needs a pair of numbers with a meaning and intuition attached to them.
When multiplying fractions, the numerators (top numbers) are multiplied together and the denominators (bottom numbers) are multiplied together. To divide fractions, rewrite the problem as multiplying by the reciprocal (multiplicative inverse) of the divisor. To add fractions that have the same, or a common, denominator, simply add the numerators, and use the common denominator. However, fractions cannot be added until they are written with a common denominator. The figure below shows why adding fractions with different denominators is incorrect.
I agree with Mike’s comment. As I read the post, I thought about how students could also arrive at invert and multiply by a fraction by exploring the patterns of dividing whole numbers by fractions. Students could look for and make use of structure as they move from whole number/fraction to fraction/fraction. Coupled with a context, students will obtain a great grasp of this concept.
Forgot to mention the following in my first comment!
The idea of creating that shortcut is also based on the understanding of fractions as division (as Julie mentioned above) and is why in 5th grade we limit students to division of whole numbers by unit fractions and unit fractions by whole numbers. If we can help students understand that 1/4 means the same thing as dividing by 4, then creating that whole for the denominator makes so much more sense because I know to get a whole, I need four quarters (so multiply by 4).
Great post, Graham. One important thing to note, I think, is that the models you created for the understanding of your readers were created based on you trying to understand this better. For students to do this, they need a context – and you get this more than just about anyone I know. Teaching these procedures without building the understanding behind it can be as damaging as K-C-F.
As always, a great post!
Spot on Mike! The context makes this idea much more accessible for students. Glad you chimed in here bud, cheers!
Thanks for this thoughtful progression – (as well as the others) that have been beneficial to teachers. One comment that I have is that in your model you change the size of the whole to create “common denominators” which I think is covered very nicely in Fawn’s post, but if others don’t go back and read they not think intentionally about the size of the whole that they start with. In your picture you are using a proportional rectangle to your originals, but that concept comes later. Thanks for your work on this.
Such a great point Kristin. I hope people do go back and read Fawn’s post but you never know. You can lead a horse to water…..
I personally like this, but I feel dubious about how it would work with my sixth grade students. Maybe this varies by district, but I don’t think my students are at all familiar with complex fractions like this. In fact, they seem shocked that fractions and division are even related (even though, as you point out, 5.NF.3 should have covered that), and don’t know about reciprocals till I teach them. However, they do generally have a good grasp of visual models of fractions and the meaning of fractions as a share of one or more wholes.
I agree with the first two comments — whole number divided by unit fraction is an excellent place to start. Then I have them go through whole number divided by non-unit fraction (e.g. there must be 1/3 as many 3/5s in something as there are 1/5s, because 3/5 is 3 times bigger). Once we have established the concept that dividing by a fraction (or whole number) is equivalent to multiplying by its reciprocal, we do some simple examples of fraction divided by fraction to demonstrate the same ideas apply.
My personal feeling is that if we taught/emphasized the concept of inverse operations earlier and better, fraction calculations would be easier to work with and understand than they are with the visual models which Common Core and/or my district’s curricula emphasize so heavily. I do like the visual models up to a point (including for whole number divided by unit fraction), but it frustrates me that kids often get stuck on them even past the point when they are inaccurate and difficult to understand. If my kids had more background knowledge of fractions as division and multiplication and division as inverses of each other, I’d prefer to teach it your way.
Thanks Julie for sharing your thoughts.
Personally I wouldn’t except students in 5th grade to understand complex fractions but I think it should be an expectation that students have had an ample time exploring fractions before the get to 7th grade.
The lack of exploration in the elementary grades is what killing our fractional understanding . I really think the major underlying issue here is the rush to procedural thinking as opposed to thinking of fractions as parts of the whole. I would think the idea of teaching inverse in the earlier grades would be too abstract for many students to understand, let alone grapple with but I could be alone. I’ve never tried so it’s tough to make that call. My wheels are turning….thanks.
Try using Engage NY curriculum or parts of it if your district allows you to use other resources or supplement your curriculum . They do a nice job of introducing the underlying concepts of fractions. You will however, need to teach the conceptual understanding of dividing fractions.
I can’t wait to share this with my teachers. I especially like the idea of multiplying by the number that makes the denominator into one (the inverse of the denominator).
On Tue, Aug 2, 2016 at 2:00 PM, Questioning My Metacognition wrote:
> gfletchy posted: “As elementary teachers, we rarely have the opportunity > to explore division of a fraction by a fraction. When we do, it’s normally > accompanied with Keep-Change-Flip or the saying “Yours is not the reason > why, just invert and multiply.” Both are conceptua” >
Love to hear how it goes Susan. Please share whatever you can after you take it for a test drive.
I would begin with lots of examples of whole numbers divided by (whatever the word is for) fractions w/ 1 in numerator.
Exactly the comment I was going to leave. It makes sooo much sense that 3/ 1/2 is 6 or 2 / 1/4 is 8. You can see it!
When mathematicians make sense of this, they use the inverse idea a lot. 2 / 1/4 is asking what times 1/4 is 2? Whatever is 4 times the 2.