As teachers and students ramp up for testing I was invited to visit a 5th grade class and asked to focus on fractions. Before the lesson, the teacher and I discussed the importance of a number line, which was an extension of a conversation we had a couple weeks back. We decided to start the lesson by throwing this on the board.
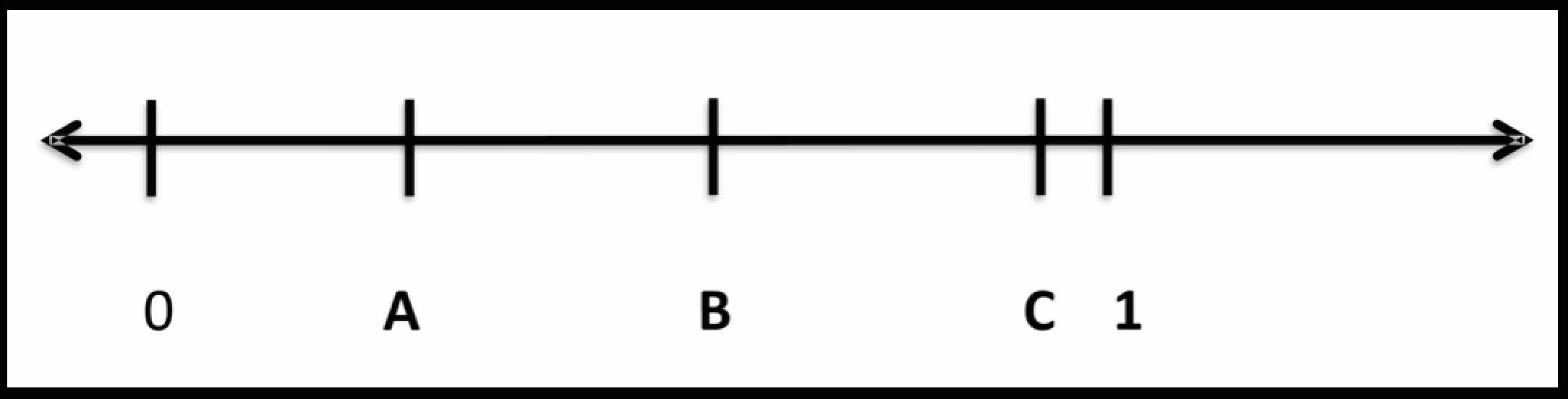Everything went as planned. Students were able to determine and justify the correct location of each letter.
A = one-fourth B = one-half C = ten-elevenths, eight-ninths, fourteen-fifteenths
We accepted various answers for “C “and were thrilled that students could justify about the numerator and denominator being really close to one another. Then we showed the next number line and the rest of the lesson went to “hockey sticks and handbaskets.”
Student responses for the location for “A” and “B”…
We blamed it on zero…or lack of it.
With the lesson plan out the window, we quickly improvised and went to a Number Line Number Talk. I don’t know where it came from, we just made it up. Number Talks promote fluency and strategy and we needed both things immediately!
Number Line String-1
Knowing that the majority of student understanding hangs on zero, we started there.
They nailed one-half so we went here…
Students: The number line shifted a fourth and the “x” is still in the middle, so the “x” shifts a quarter greater than one-half to 3/4.
Then we moved on and the same reasoning was applied to locate the “x” at 1 whole.
So far so good. If SMP#3 was a person, he would have been proud of these students as they reasoned their way through the number line strings.
Then we dropped this one on them.
This one stung for a minute.
Students were given time to collaborate and discuss in groups about the location of “x”.
Student: Well, it has to be greater than 1 whole, but it’s not quite 1 and 1/4. It’s halfway and half of a quarter is 1/8. So it’s 1 and 1/8.
We went nuts. Kids went nuts. Math was happening and everyone was happy. “We want another one!” was the chant around the room.
Number Line String-2
Not a problem. So we moved on to this guy…
About half the class was immediately able to use their reasoning from the previous number string to locate the “x” at 7/8. We picked up about another quarter of the students through the explanation. Some students were completely lost a this point (note to self “see you in small group”).
Then we showed this one…
I’m not going to lie, about half the students were completely lost by the time we arrived here. What I loved most about this process was that students were still discussing and persevering! That’s a winner in my book.
I was hesitant… but we did one more because they wanted it.
Because these number strings were created on the fly, students found an unintended pattern.
- when the number line began with 1/2 the “x” was located at 3/4
- when the number line began with 3/4 the “x” was located at 7/8
- when the number line began with 7/8 the “x” was located at 15/16
- when the number line began with 15/16 the “x” was located at 31/32
The students identified that if the pattern continued the denominator doubles and the numerator is double plus 1. (Freakin’ nuts)
So we tested our luck again with the number line from the beginning of class…
Me: So can we use what we just did to find out where “A” is located. Anyone want to change their answer?
Student: Halfway between 1/2 and 2 is 1 and 1/4. If we jump in one quarter on each side it would be at 3/4 and 1. Halfway between 3/4 and 1 is 7/8.
From the 24 students in the class, only 3 were able to make sense and repeat what the student shared. We started with zero understanding and 1-hour into the opener we had 4 kids understanding and a ton of work left to do!
My takeaways:
- At most, this is a DOK 2 question but it really chewed brains.
- Students need more exposure with number lines that don’t start at zero. The number lines I encounter, typically begin with a zero which can give a false-positive of student understanding.
- The number string highjacked the entire lesson and that’s okay.
- Understanding benchmarks and how to use them are the underpinnings to solid fractional reasoning.
- These Number Line Strings are wicked awesome for building fractional reasoning. If they’re out there please show me where I can find more. I want more. If you created them, I promise I didn’t rip you off and want to give you full props. I’ve just never seen or heard of them.
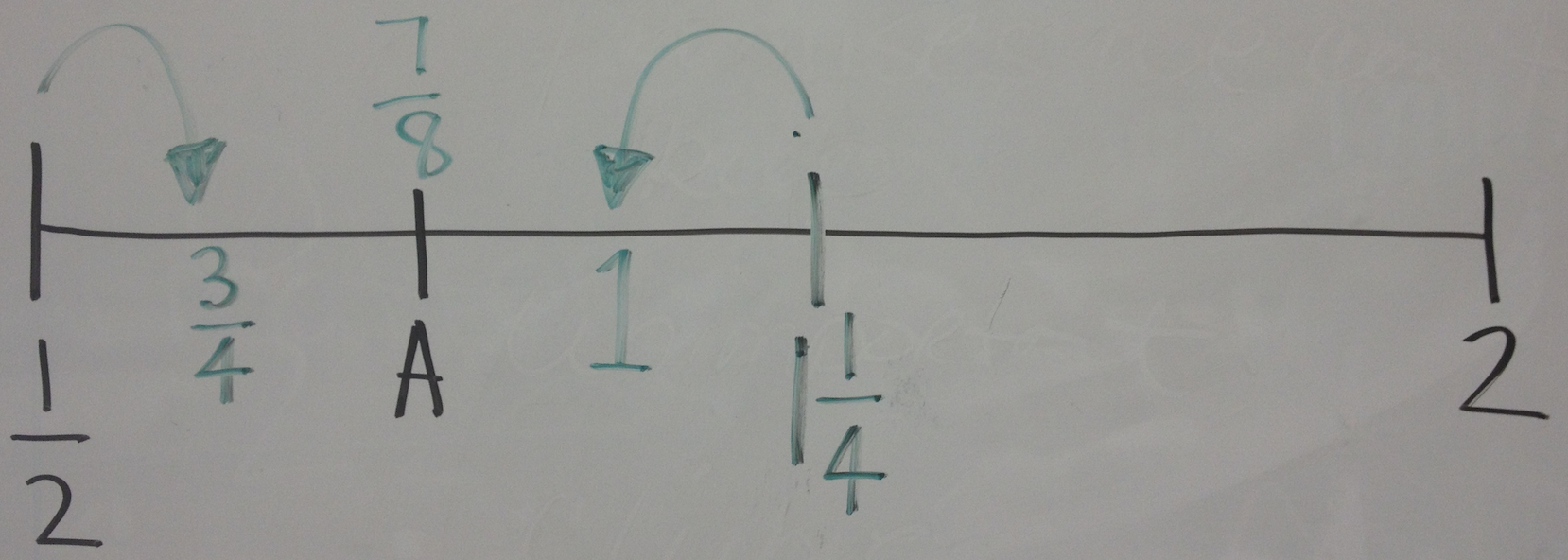
I shared your post with my 3-5 teachers and I had a 3rd grade teacher immediately respond that she wanted to do this with her students.
So, we started by modifying the second part of your lesson to ensure we met her students needs, but also with an idea of how to press, if needed.
We began her lesson with the first number line you shared with your 5th graders. Exactly the one you have in this blog. When printed, it did come out as precise as we were hoping, but we went with it. The students went nuts! During the discussion, the concept of precision and equivalence kept resurfacing as students tried to measure it as fourths first and then thirds. They weren’t happy about the placement of the one on the number line. However, one student piped in to say that we can’t change the number line to fit our answers, we have to find the answers that fit the number line.
The students reasoned that the maker of the number line meant to have it be 1/4, 1/2 and 7/8. But, they weren’t very precise. another student shared that it could be 1/3, 2/3 and 3/3 and the one was a mistake and should not be there.
The teacher focused on the students perseverance to identify the precise measurement of all pieces when related to each other and that they didn’t have to tools at that time to determine the precise fractions for each point.
Then, she moved on to the fraction lines with an x in the middle. We changed the mixed fractions to improper fractions to see how they grappled with them. ( 0-1, 1/2-3/2, 1/4-5/4, 1/2-5/4) A major over-generalization occurred. The students added 1/2 each time to the first 3 number lines and it resulted in an accurate response. While some students identified the distance between the starting point and the ending point, most just immediately added 1/2 to the first fraction and then another 1/2 from that answer.
Tomorrow we work on the last number line. We can’t wait to see how they problem solve through renaming the 1/2 and finding 1/2 way between 3/4 and 4/4…if that is even how they proceed!!
So, thank you for providing an amazing opportunity for our 3rd graders to engage in amazing discourse, attend to precision (especially with fractions), reason abstractly and quantitatively and to begin noticing a pattern.
I really enjoy your blog and following you!
Reading this comment made my my day! Thanks so much for sharing this Sarah.
I love that your 3rd grade teacher was on-board and wanted to try this out with her students because it’s these opportunities to engage with fractions that many 3rd grade students never experience. I’ll definitely be sharing your comment with some 3rd grade teachers in my district to help give them a small nudge:-)
The best part…”we can’t change the number line to fit our answers, we have to find the answers that fit the number line.” Pure gold!!!
Wow — this is the epitome of constructivist teaching! I’m a musician and this experience reminds me of jamming with friends and not knowing exactly where the song is going, but trusting the synergy between oneself and the other musicians (and perhaps even the audience – however, we rarely had those when I was playing!). 🙂
So cool that you and the teacher were willing to allow the students’ conceptions/misconceptions and curiosity to dictate the direction of the lesson… I was just in a 3rd grade classroom that was working on a very similar concept, but they had to find 1 on a number line given a fraction (we started with a unit fraction, and then progressed to non-unit fractions — both less than 1 and greater than 1). Very eye-opening to see some students initially reason that 1 “always goes at the end of the number line because that’s where it always is” regardless of the given points and values! Just reiterates your 2nd bullet point about the necessity for variation in order to push understanding and reveal misconceptions… as well as the IES practice guide recommendation #2 for improving fraction teaching and learning in the U.S.(http://ies.ed.gov/ncee/wwc/pdf/practice_guides/fractions_pg_093010.pdf)
Beautifully done and well-described! Thanks for sharing, G!
Thanks Brian! I work with some amazing teachers here and we really try to stress to each other the importance of “trusting the process.” In doing so, the lesson plan sometimes goes out the window and we’re ok with that.
I frequently wonder how many student misconceptions are generated by us as the teacher. Definitely not our intention but I believe it happens a lot.
Love the little gem of the link you shared. I found it a while back but thanks for putting it back in my face. I need to keep it closer.
Cheers!
Ooooh. I love this. The empty number line string that I use in my classroom as part of our morning routine uses fractions, or it did when I taught 3rd grade. Students came in and had different fractions on their desk that they had to place in the right spot on the string. Stunk for the first kid that had little to no clues and for the last kid that had to move all the cards so his would fit, but learning occurred!
I’m sure your 3rd grade students miss You and the fun you brought to their class….even when it was a struggle. I guess I can begin waiting for your next blog post to see how you’re using the open number lines that don’t start with zero in 2nd grade.
I just started holding my breath…please don’t make me wait long.