My daughter has laid down a marker when it comes to reasoning with fractions. Well, at least in my small world. She’s 10.
She won’t read this post for a long time because her mom and I know what she reads on the internet…at least we hope we do. Maybe she’ll never read it but I know she has great things in store and that makes us proud.  There might be a day or time when she feels defeated or maybe doesn’t feel like she has anything to contribute.  If that’s the case, I’m keeping this nugget in my back pocket.
In my 14 years of playing math with students AND teachers, she did something that teachers don’t teach, textbooks don’t show, and test prep academies might never understand. We were working on a task which led us to a parallel question.  I want to share the sequence of events that took place.
We started here…
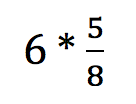
Solve the problem BEFORE pressing play and think about how you solved it.
What the hell just happened?!? Â I get it… but what the hell just happened?
When she said “I don’t like multiplying fractions” IÂ immediately thought she was going to jump to some trick or algorithm she’d been taught in 4th grade. I wanted to know more so I asked her to explain.
Partial products for multiplying fractions! I’ve never seen a student or teacher use this strategy and to be completely honest, I’ve never thought of it myself. But it’s beautiful and makes perfect sense.
Lesson 1: Don’t let anyone tell you that you have to multiply straight across when multiplying with fractions. Partial products work just as well.
With this being a student invented algorithm I wanted to try and break it. It’s what we do. Â So I changed the 6 to a 7 because it isn’t so tidy when divided in half.
Another little gem of understanding was uncovered. Any predictions?
Silly me. It’s a student-invented algorithm so she owns the understanding. Â Everything she’s doing here has me vigorously nodding my head in agreeance.
Lesson #2: Don’t let anyone tell you that you need a common denominator to add fractions. Partial sums work just as well.
Let’s change the other factor and see how you tackle it.
She didn’t do 60 questions in a minute. In fact, she never has because that’s not our jam. I don’t think anyone would argue that our daughter isn’t fluent.
Lesson #3: Don’t let anyone tell you fluency = speed.
If the definition of fluency asks students be efficient, flexible, and accurate she nailed it. So why is the definition of fluency different when we talk about addition and subtraction or multiplication and division of single digits? The same way our daughter decomposed numbers and used distributive property with fractions is the exact same way she learned her basic facts. Her understanding of number is scalable.
We started slow and took our time when she was in kindergarten because the turtle always wins the race. As our good friend Tracy Zager says, “The ROOTS of the work are in K. The FRUITS of the work are in 5th”.
Lesson #4: Memorization of facts and algorithms is a learning objective stopgap. It will never prevail in the long run.
Our work is paying off and I’m a #prouddad.
May I use this with my pre-service maths specialism primary teachers? They are so indoctrinated into using standard algorithms it is difficult getting them to think differently.
The article reflects on a unique and insightful approach to fraction reasoning demonstrated by the author’s 10-year-old daughter. The daughter invents a method using partial products for multiplying fractions, challenging conventional algorithms. The author highlights valuable lessons learned: the flexibility of multiplication with fractions and the effectiveness of partial sums for addition without a common denominator. The daughter’s understanding of fluency challenges the notion of speed, emphasizing efficiency, flexibility, and accuracy. The narrative underscores the importance of a gradual and deep understanding of mathematical concepts starting from kindergarten, promoting a scalable understanding of numbers.
Always great to hear her math thinking! She does own the understanding and can apply it to multiple situations and contexts. The roots of the work ARE in K. But the fruits grow far beyond 5th! #proudfriendofaprouddad.
WOW, what strategic thinking! I am otherwise speechless…
Love this Graham. If I have got anything from being part of Cathy Bruce’s research into fractions is that being able to use fluency and reasoning in fractions is super important. This is exactly why I really love Cathy Humphries book “Making Number Talks Matter” , it really stresses this point, that the distributive property (and other properties) hold true with whole numbers and fractions. There are some examples in the book how the strategies you use on whole numbers can then be applied to fractions.Some great inquiry opportunities to allow students to explore and discover this just like your daughter has! I also love that your daughter allows you to do math with her! My daughter runs for the hills when I start geeking out about math. LOL. Thanks for sharing.
My mind is still spinning and I am trying to follow her-which I love! I see the importance the understanding of unit fractions in her addition process!
This was the most wonderful article you’ve posted yet! I loved the video of your daughter reasoning her way through this. Thank you for sharing.
Thanks for sharing this!
Awesome! Thanks for sharing.
All I can say is WOW! Not only does she demonstrate fluency, she has such a deep understanding of number in general. I think you should take her on the road with you to help teach teachers! 🙂
Wow. That is SO wonderful! I’m going to show my teacher candidates this too!! Thanks so much for sharing this with us.
I’ve heard fluency in a language being described as whena person can create a joke or a play on words in that language.
What she did mathematically was just that…it’s as creative as a beautiful play on words…and makes me smile in the same way.
I doubt we would define fluency in a language as the ability to repeat conjugated verbs quickly…perhaps there is more here to discuss. Bravo for bringjng this example to light.
This is what real math is all about! Thanks for sharing!
Holy! I love this approach! Thank you, mini gfletchy.
Oh wow. Love this fluency right here. Awesome!
Love this. Thanks for sharing!
When the time comes, you can tell her that she taught something about learning and teaching math to a group of 8 student teachers in California.
Was she originally working on homework and you noticed what she did and started recording and asking her questions? Or did you actually give her the first question? I’m going to guess it’s the first. And I’m impressed that she actually deviated from finishing her homework to becoming Dad’s student/actress. Beautiful!! Truly a Fletcher!
On Wed, Aug 30, 2017 at 10:13 AM, Questioning My Metacognition wrote:
> gfletchy posted: “My daughter has laid down a marker when it comes to > reasoning with fractions. Well, at least in my small world. She’s 10. She > won’t read this post for a long time because her mom and I know what she > reads on the internet…at least we hope we do. Maybe she’” >