There’s no denying the power of the Post-it. Many brilliant minds within the #MTBoS have harnessed its’ power to help students make sense of mathematics and this week was no different.
Only this time we infused them into a Marilyn Burns must have…

Coffee stains & post-its. The signs of a great read.
To start we had students build animals from pattern blocks and had partners guess the animal.

A rabbit???
Some students were not sold on their partner’s creation which lead to some heated discussions. Score a point for SMP3.
I showed my animal and we decided that it looked most like a dog.

My dog on DAY 1. The tan rhombus was the tail.
I built the dog to show what it looked like on day 2 and 3.

The document camera didn’t want to play so we took it to the floor.
Teacher tip from Mike Wiernicki: if you have foam pattern blocks you can wet them and they’ll stick to your dry erase board…unfortunately these were wood.
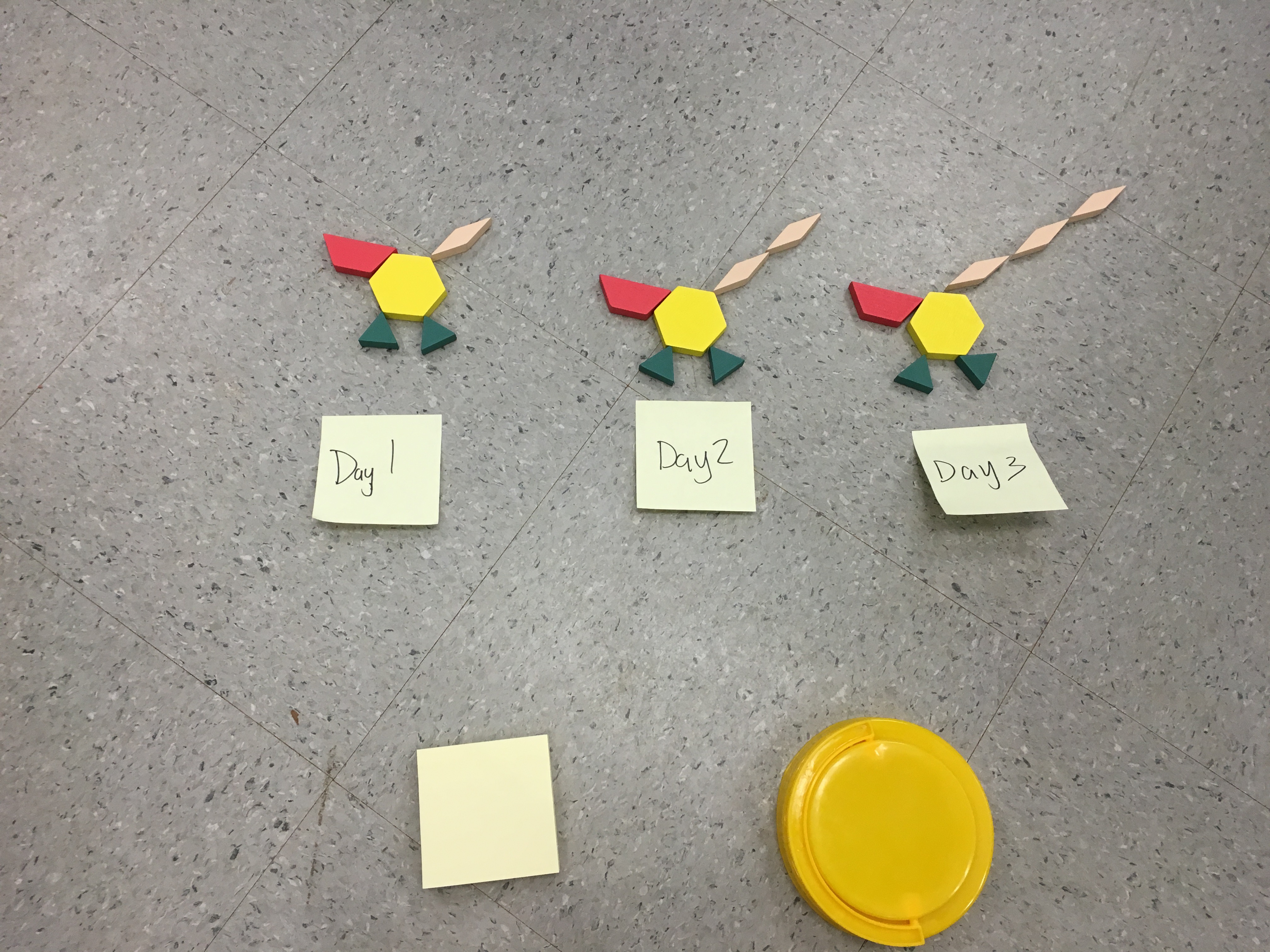
The first 3 days
Then we asked… What do you notice?
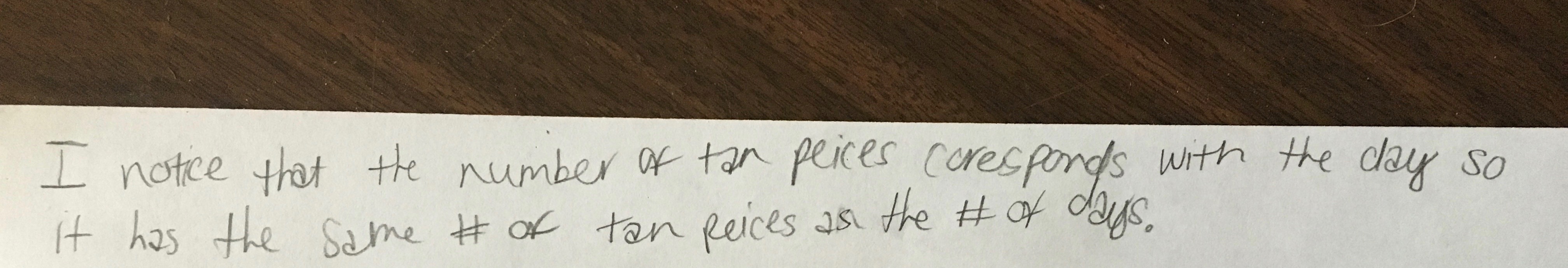
And we followed that up with, “What will the dog look like on day 4 & 5?”

Students began building the dog for days 4 and 5.

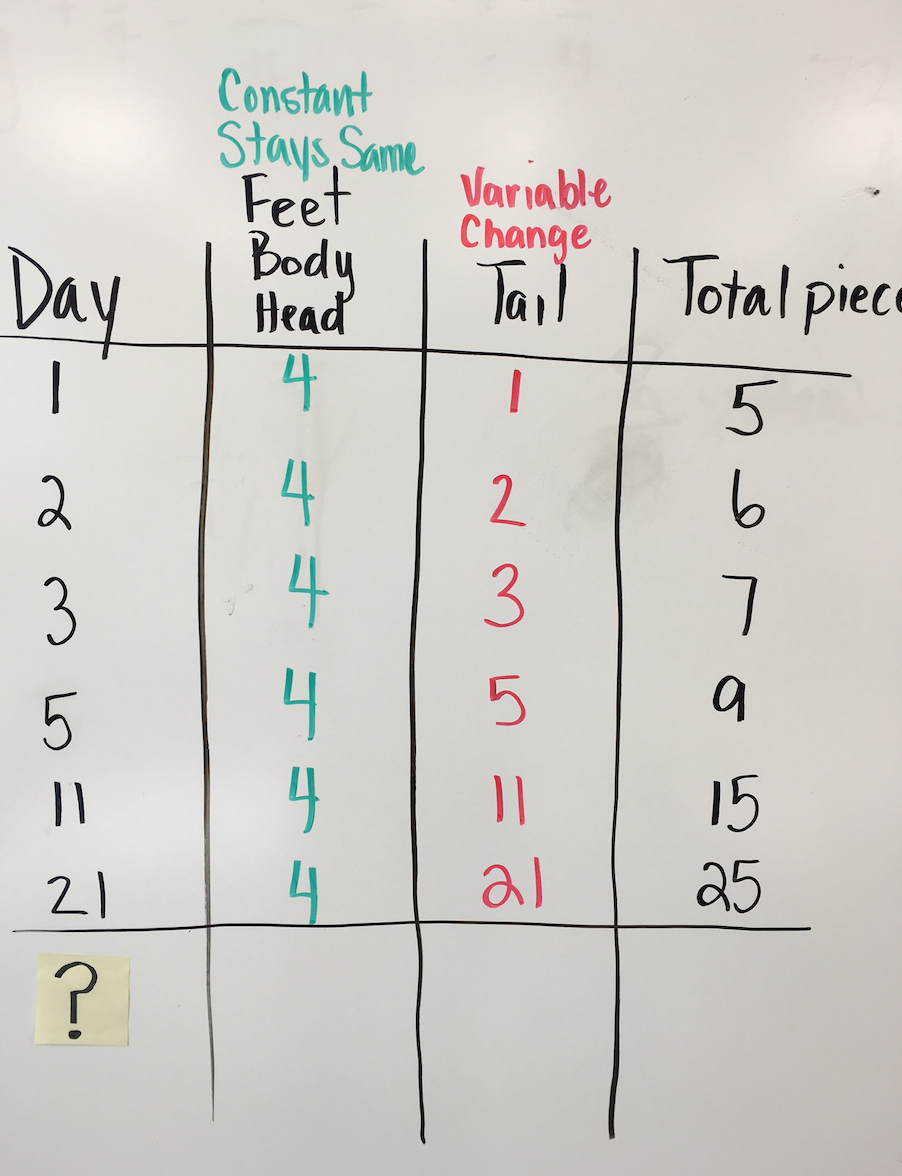
We asked students to organize their thinking in a table and this is what they collectively came up with:

This was a great opportunity to pull out specific vocabulary with students:
- Students said “The body, head, and feet never change. They always have the same number of pieces.” The term CONSTANT was introduced.
- They also noticed that “The dog’s tail grows one rhombus for every day it’s alive.” VARIABLE was introduced.

We had students find the total number of pieces for the 11th and 21st day.
Student: Do we have to build it?!? That will take forever. What if we don’t have enough pieces?
Me: Can you use what information you already have to figure it out?

The table really helped students recognize vertical AND horizontal patterns which are typically harder to find. We were really surprised by how quickly students found shortcuts to complete the table.
What they noticed…
- The head and body column never change so they placed 4s all the way down.
- The number that went in the tail column matched the number of days.
- The total number of pieces goes up by one each day it grows. (recursive rule)
- The total is always 4 more than the day. (explicit rule)

Share your thinking.
For the most part, students did an excellent job completing the table…when the days were identified. But when we added a Post-it to the day column things went a little sideways.
Students: Hey! That’s not fair. We don’t know what day it is.
Me: I know. It’s my mystery number.
Big shout out to Mike for introducing me to the Post-It variable.
Student: We can’t finish it without knowing the day.
Me: So give up then! I guess there’s no way for you to tell me how many pieces there will be on the mystery day.
The students began talking amongst each other because they knew something was up.
Student: Yes!!! We CAN do it. We know that the feet, body, and head stay the same no matter what day it is. So put a 4 in that column.
Me: Ok. What else do you know?
Student: Well since we know the tail and day always match, can we put another Post-it in the tail column and put a question mark on it just like the day column? I asked the class to check with their table and decide. Each group came back and said that’s what they wanted.
Me: What about the total?
Student: That’s easy…to figure out the total we just add 4 to the mystery number. So we just write 4 + a Post-it with a “?” mark.
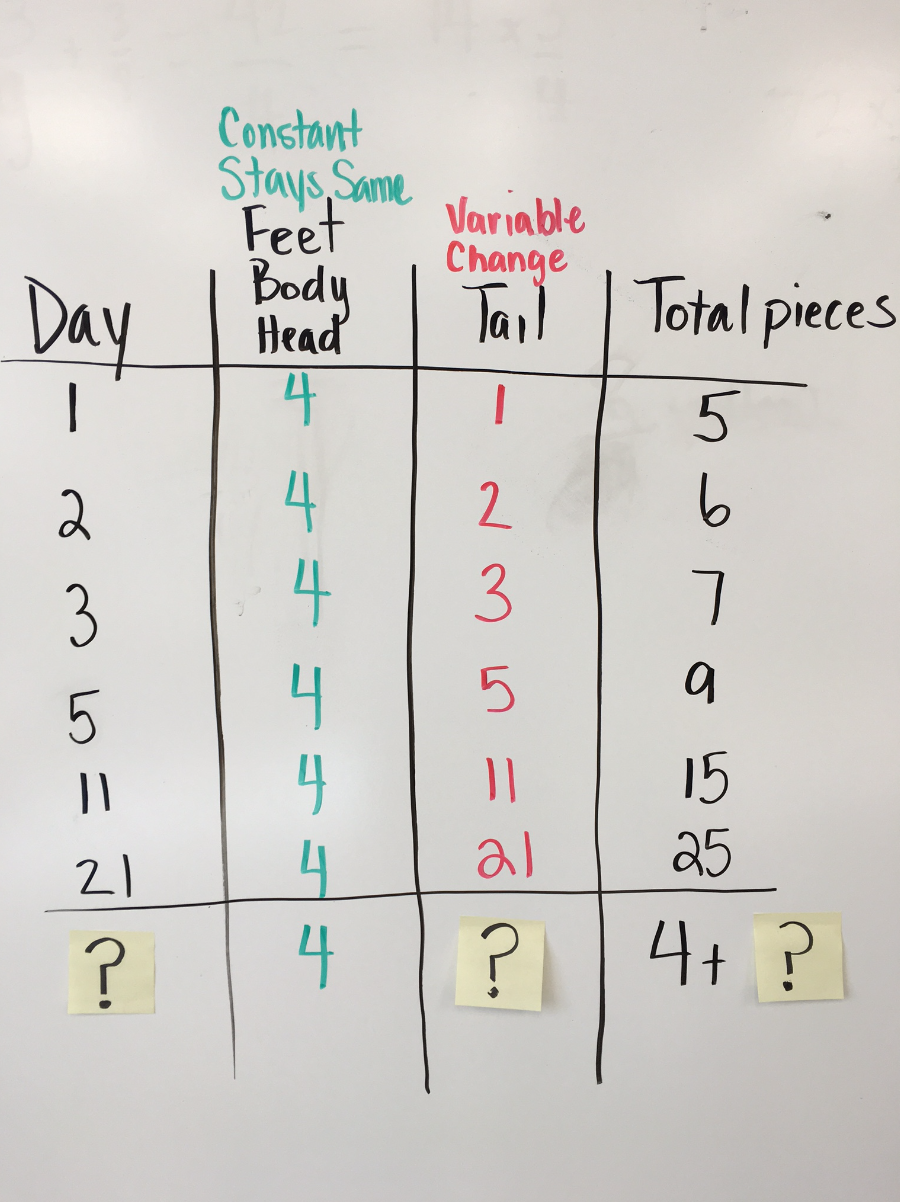
total pieces = 4 + day
Me: Oh that’s awesome. What happens if I ran out of Post-its. What could we use instead?
Student: Well you could always just draw a square and put a “P” in it for Post-it. It doesn’t matter if we have a “P” or a “?” on it because it’s still gonna be the mystery number.
I could have swore I heard math angels at this very moment. It was one of those moments I’ll never forget.

Looking back at the lesson I would definitely say it went “much too whole group” towards the end. I would have liked students to grapple with the idea of the mystery Post-it at their tables before discussing as a class. I think I just got caught up in the excitement of the moment. (note to self)
I definitely wouldn’t say that we’re Visual Pattern experts but we have till 8th grade to get there. I’m sure the early start makes Fawn happy.

This is really interesting and helpful for the students. It is not like a traditional math problem where they are expected to answer problems. Instead the students are getting a hands-on experience and they are able to control what is going on! Very impressive. I hope to include activities like this when I become a teacher,
Right on Maritza! I hope when you do become a teacher you report back and let us know how it goes. Or better yet…let us know when you start a blog:-)
Beautiful! Also looks a little familiar with some wonderful adaptations!
Sent from Windows Mail
This makes me smile because it was probably my favorite class I took at UGA with you. Love the way I’m continually making connections back to what we learned. Thanks Dr. O!
I never tire of this lesson! It has what we all crave in a math lesson:
-low entry point
-high ceiling – I’ve taken this to quadratics and exponentials
-high interest and engagement
-connections galore – especially if you hang student tables/graphs (don’t forget to graph in the first quadrant for 5th grade) and leave it there all year for them to connect back to.
-it’s conceptual through and through – students build their understanding for constants, variables, and expressions based on what they see in the visual patterns
-after doing many of these visual patters over time, students become mathematical and algebraic thinkers. Isn’t that what it’s all about?
-and now, with technology like desmos, students can graph the points on from their tables to see the pattern grow on the coordinate grid.
-and then there’s the post-its! 🙂
Well done, Graham!!
I’m going to do this on Monday.I like the post-it variable lots. This will make a great continuation of our Friday lesson.
http://y4atist.blogspot.fr/2016/01/growing-patterns_29.html
I think younger children can benefit from graphing it too (mine are 3rd grade). Some of them spotted kinks in their line which gave them great feedback on how they’d counted their pattern. Quite a few couldn’t resist extrapolating a bit too.
That’s great Simon. You’re right. Graphing can be a great way for students to see the pattern another way-even in 3rd grade. And it’s another representation of a pattern they’ve already started to make sense of! A nice, natural extension. Please share the results of Monday’s lesson!
Mike/Simon,
Thanks for this because you’ve definitely laid out things we all strive for but seldom achieve in one lesson…personally speaking. Love this connection to graphing you’re both talking about and I wish I would have looked to take it there. I’ll try and revisit this idea early next week.
And Mike…thanks for introducing me to this lesson and the post-it. Great stuff my friend!
How long are your periods? I find myself doing what you described in your penultimate paragraph way too often because the end is too good to wait until the next day.
And that’s completely frustrating!
Periods vary from 1 hour to 90 minutes. I found myself pushing to the conclusion way too often so I began setting a timer to wrap up the lesson 7 minutes before time expired. Even if we didn’t get to the end of a lesson we would collectively summarize where we were in the task and students would discuss their first move when they returned the next day.
I found this really helped because if we didn’t summarize and talk about the learning it would take us 10 minutes to get caught back up to speed when we returned.
The timer kept reminding me to not rush…the turtle won the race.
Please share if you have other suggestion Glen and thanks the comment.
Yes, some lessons can be better continued, better sometimes. And I agree, that it helps to wrap up properly at the end of the lesson. Hard to get this timing right though sometimes (I usually have an hour).
I was wondering that too Shannon. I am thinking I’ll try this with my grade 3 students.
Yes! Go for it Marge because this is definitely doable in 3rd grade.
What grade did you do this in? This is amazing!!!!
Thanks Shannon. This was done with a mix 4th and 5th grade class but the idea of the lesson was originally introduced to me when I was a 3rd grade teacher by my math coach Mike Wiernicki. I think this would work in any 3-5 classroom and the results would be relatively the same.