I think about the question mark every time I teach a lesson.  I’ve been so carefully to get to this point. 

Yet sometimes my question mark comes from a path that looks like this.

The opening part of the lesson is over and the work session is well underway.  It’s the time when I lose kids or they preserver to the point of productivity.  It’s really tough to make a teaching move that helps save my question mark.  The question mark is my next move.

I try not to corner myself.

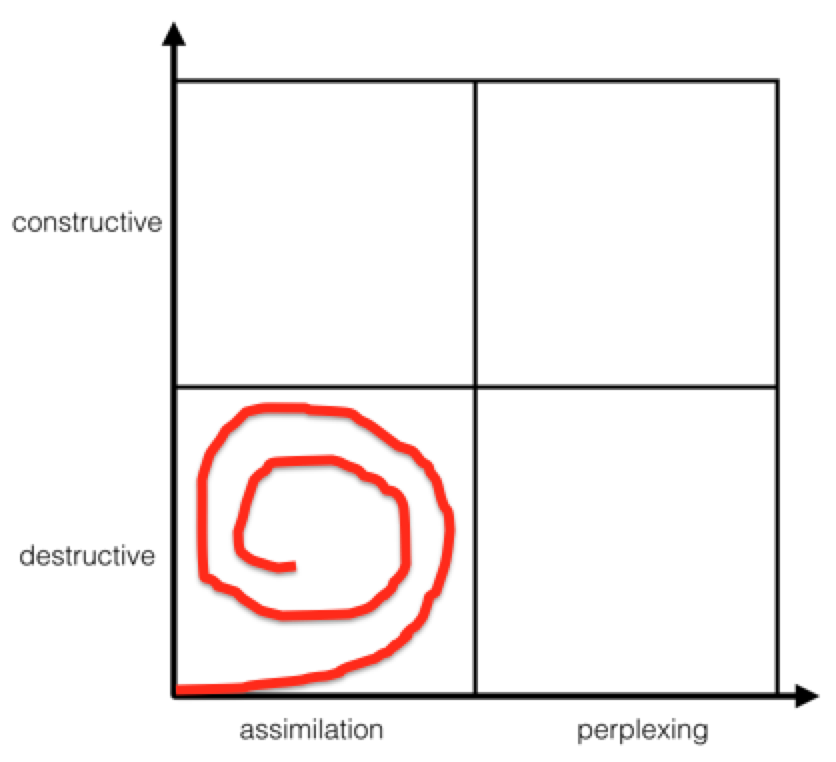
Knowing this time would come, I trust the task.  The tasks I choose determine the path of my question mark and where the learning will go?  If my question mark comes from a spiral pattern, I have a lot of backtracking to save it from Davey Jones’ Locker.  It’s where my lessons go to die.

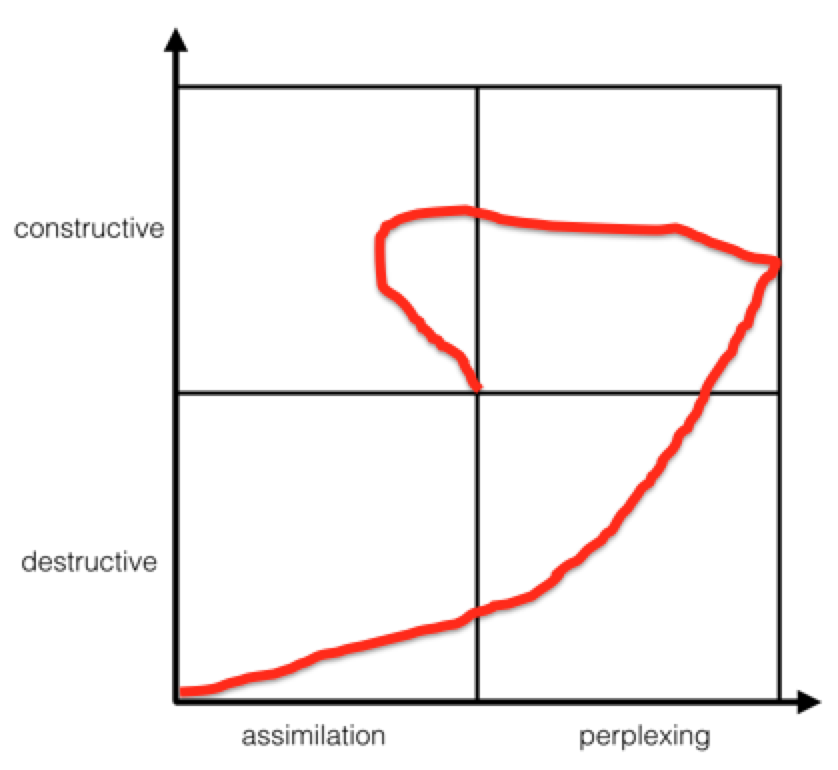
In every lesson there are instances that separate the constructive and destructive struggle. You can see students cross from one box to another.  Lots of times, lessons end up being destructive because students don’t care to preserver (most of the time it’s my fault).  If I ask students to continuously engage in tasks that require assimilation they become bored (my fault again).

A big thanks to Dan Meyer for the perplexing introduction to perplexity. 

Perplexity and disequilibrium are extremely similar, yet I see them as totally different in terms of engaging students.  I try to never let the disequilibrium be destructive.  I do that by purposefully constructing disequilibrium through a perplexing situation.

Disequilibrium is uncomfortable.  Perplexing is a challenge or puzzle.

Perplexity stems from non-routine.  Since perplexity has made its way into my teaching practice, productivity has found its way into my classrooms.  Manipulatives and modeling with mathematics are required because students need them to make sense of non-routine problems.  Non-routine means that students are placed in a state of perplexity and unfamiliarity.

Dan Meyer and Robert Kaplinsky have spoken at length about unfamiliarity and where explicit teacher moves are pivotal in keeping students engaged in mathematics. Choosing the right tasks, such as 3-Acts and OpenMiddle, empower me to better control which box my question mark will go to next.

Where do the tasks you choose take your students?