I was talking with a group of 5th grade students today…
Me: You know that next year you’ll need to be able to divide a fraction by a fraction and not just a fraction by a whole number? (MCC6.NS.1)
Student: I can do that right now Mr. Fletch! I don’t need to wait until next year!
Me: Oh yeah? How is that?
Student: Well all division is, is repeated subtraction right?
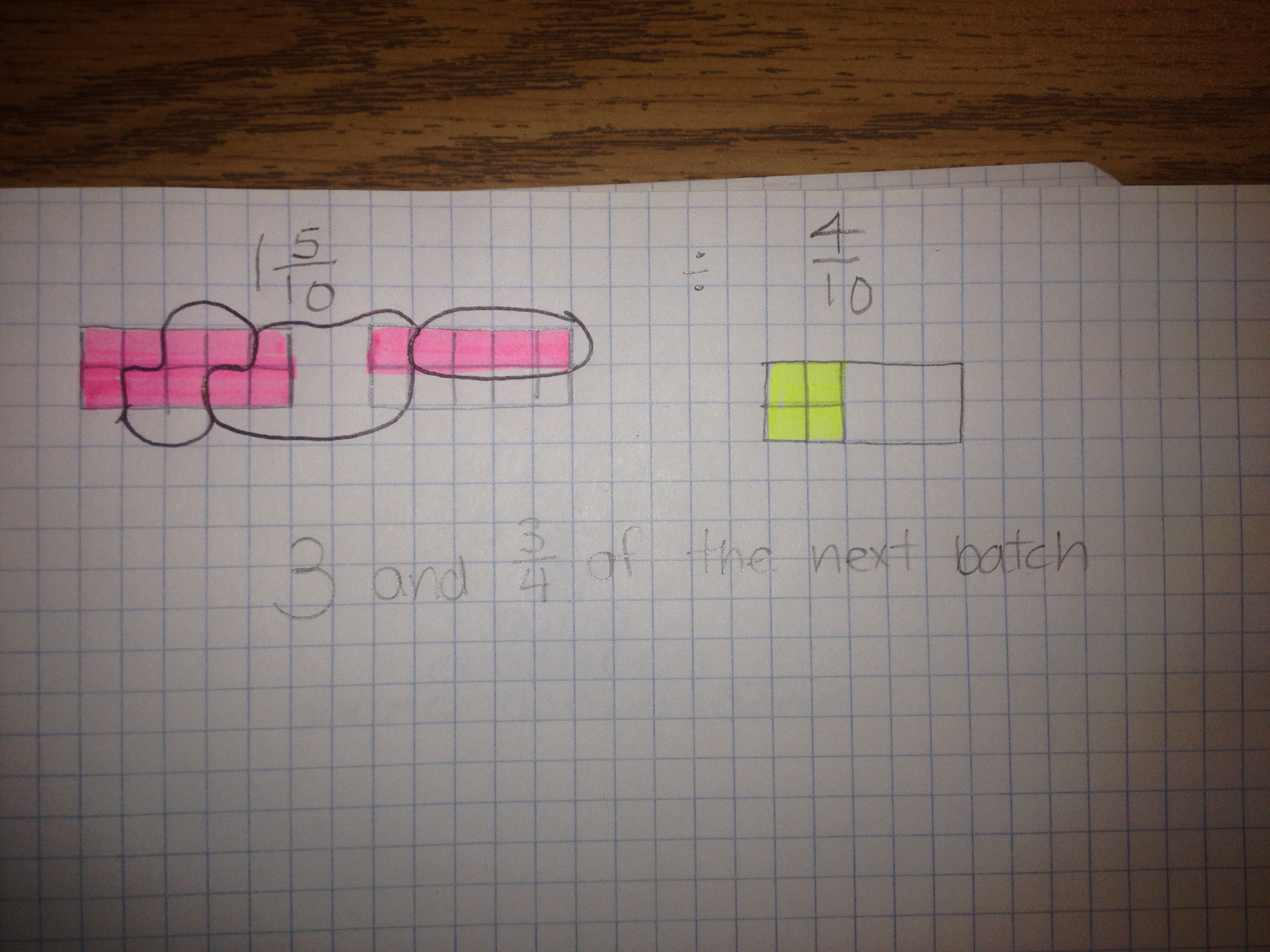
I returned 5 minutes later with the following problem and asked the students to solve it using repeated subtraction. Sam had 1 ½ cups of flour in the cupboard. He needed 2/5 of a cup to make 1 batch of cookies. How many batches of cookies can Sam make?
I didn’t solve the problem in advance and just whipped together some numbers (silly me). Having worked exclusively with models to this point and never attempting repeated subtraction myself for fractions, I thought it would make sense. My understanding was that repeated subtraction and division went hand-in-hand although it’s not the most efficient method…but an accurate one. The student’s solution.
Everything looked great! I quickly changed the mixed number into an improper fraction, inverted then multiplied. Yes I know it’s super procedural but I wanted to quickly check the students solution (disclaimer: I understand why invert & multiply works so I’m okay to use it).
Me speaking to myself: And the answer is… 3 and 3/4. WHAT THE?!?!?! How is that?
I repeatedly looked at the student’s work and double checked it to make sure he had made no errors. Everything made sense which completely baffled me and then there it was!
Me: Draw a model to represent what you just did.
Student: But I have 2 different answers and I know my drawing is right.
Me: How many tenths make a batch and how many tenths are “leftover”?
Student: Well I need 4/10 and I only have 3/10 and (the light-bulb explodes)……..Oh I get it! It takes 4/10 of a cup to make a batch and the 3/10 in the repeated subtraction is 3/10 of the 4/10 needed. So I have 3/4 of the next batch. So the answer’s really 3 and 3/4 of a batch!
Rule: if you can’t make sense of your thinking through a model, you probably don’t understand!


good job beautiful work
i dont get it
Turtle and Katie thanks for the encouragement!
What I found most awesome about this student was that in order for him to use repeated subtraction he had to identify a common denominator. I really like the idea of this because the subtraction/common denominator piece lends itself to a tidy model.
It would have been really interesting to see how he would have approached the modeling of division if he didn’t think of repeated subtraction.
This student was definitely rocking the SMPs! What a beautiful example of the necessity of context! Awesome job gfletchy!
Well done, g and 5th grade partner in math sense-making.
Beautiful, elegant, inspiring. Just like you!