Cardinality…what is it and what does it look like?
If you’re not a kindergarten teacher you might be left shrugging your shoulders if someone asked you to define cardinality. Before students can own the idea of cardinality, they need to have an understanding of one-to-one counting.
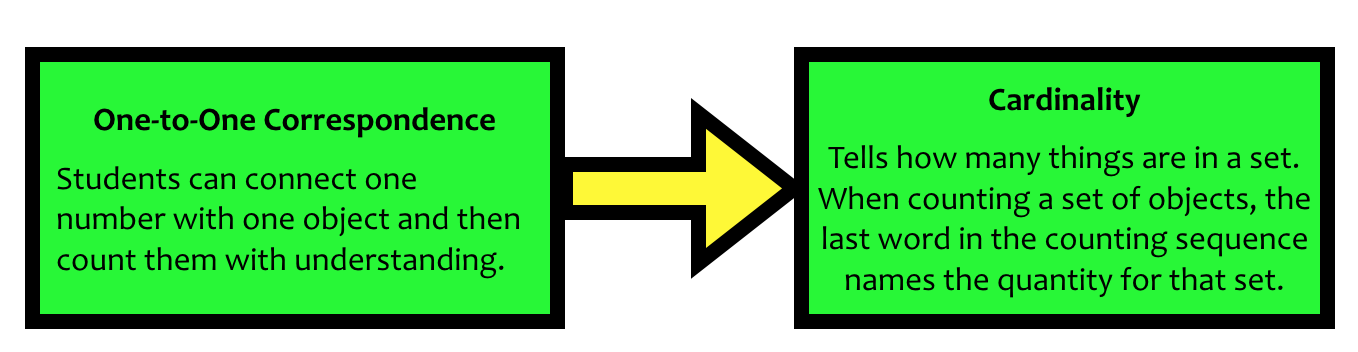
So now you know what it is, here’s an example of a 4-year-old working to gain an understanding of cardinality…
If you’re not familiar with cardinality you expect this little guy to say “seven”. Especially after he’s counted and I’ve repeatedly ask him “how many are there?”
But nope, he’s not quite ready.
Be the teacher…
What activities and/or suggestions can you offer to help me move this little guy from 1-to-1 counting to cardinality?
Please share you thoughts in the comments. My hope is that by sharing this video parents can begin to look for and promote cardinality at home before students get to kindergarten.

Thats really interesting and playful ideas I must have to try , thanks to all for sharing .
This video really helped me understand what I had read about on this topic (it didn’t fully make sense to me when I read the definition of cardinality). I’m a new, incoming teacher. I student taught in third grade. I was curious how you would help a third grader with the following issue: If you asked how many items there are, she’d count them, say, 7. Then if you ask her to add two more, she’d have to start all over at 1, count back to seven and then count the next two. She was stuck in the pipeline for special ed testing and I wondered how I could have helped her while she wasn’t getting the help she needed from more of an expert. How would you practice with a child like that who just couldn’t get it? If you asked her what 5+2 is, she’d have to draw five dots, draw two dots and then count them all from the beginning (in third grade).
Thanks for the comment and question ER.
I think a lot of the strategies mentioned here in the comments are great ideas that I would use with your 3rd grade student. When you introduce the idea of 2 more children go through a series of stages.
1. They physically count all dots starting from one.
2. They image and count all dots starting from one.
3. Count on from one number.
If you happen to have another student next year that struggles with joining and adding sets, try the aforementioned strategies and let us know how it goes.
I’m so glad to have come across the question asked by ER, and your reply gfletchy! I am trying to teach a 3rd grader with the same issues. She was tested for Spec Ed and didn’t qualify. Ugh! So, she is in my regular education 3rd grade classroom and “struggling” is an understatement. I plan to try your strategies next week!!! Thank you so much!!!
Love to hear how it goes. Please report back and let us know.
Hello gfletchy how are you doing? You are doing great job like us. Kid voice so sweet he was counting very well 1 2 3 4 5 6 7 nice one and you are motivate again and again great…!!! I am also teacher and went school also work for this https://www.facebook.com/mymathdonecom/
Something that I think might have made a difference in him saying 7 instead of counting again, would be to take another set of 7 things, and ask if the two sets had the same number of things. This comparing activity might spark the idea that we can match things one to one, and if they the sets have the same size, then they have the same number of things.
Oh nice! I like the idea of comparing because of the massive role it plays in the developmental stages of building and understanding numbers. This makes me want to give it a try. Thanks!
One thing that made me be able to understand cardinality was the activity of the bucket. This activity consisted of counting the objects and then putting them inside the bucket. I found this very useful since it leads the kids to understand cardinality. One thing that I also noticed is that now that I am in college in order to understand cardinality for Discrete Math this activity helped again.
Thanks for chiming in here Alicia. The counting bucket is a staple and I’m really glad you’ve mentioned it. Thanks for sharing!
When I was barely tall enough to peer over the Albertson’s checkout counter, my classmates and I liked to compare numbers and engage in a debate on “which number is the biggest number ever.” The idea of infinity came up when I was in 1st grade and I started using it everywhere. Like “Dad, I want infinity Hershey bars!” Little did I know at the time that infinity isn’t really a number but a concept. Perhaps asking your child to think of the biggest number he can think of would be a good start to introducing him to the idea of infinity, which I’m guessing is the next step in learning about cardinality. Good luck!
Thanks for the comment Justin. Never quite thought about using “infinity” but the wheels are turning now. Appreciate it my friend.
Good to meet you last night after shadowcon. Now I’m creeping on your page!
Tasks that involve _getting_ can emphasize the quantity instead of the procedure:
“Let’s each eat 4 jelly beans. Can you get four for each of us?”
Eat ’em.
“How many jelly beans did you just eat?
How many did I eat?”
Source: have 5 year old.
Cheers Ben! Great meeting you too and looking forward to connecting again at NCTM Regional in Orlando.
This is a great video. I love the part when he puts his head down at the end. He is thinking, “Seriously, are you paying attention?” I do similar interviews with the Kindergarten students. I interview a bunch of students and then we (the K teachers and me) watch the videos in grade level teams and try to identify whether or not students understand hierarchical inclusion (numbers nest inside each other). We discuss: What does he know? How do you know? What would you do next?
In my interviews, I give the students a certain number of interlocking cubes. They count them. Then I give them one more and ask, “how many do you have now?” If they don’t have it, they recount, but it isn’t always obvious. One student recounted. Then, I gave her another one. She recounted. Then, I gave her another one, she recounted. Finally, I gave her another one and she sighed, looked at me like, “who hired you?” and said, ” there are 9, okay? 8 (waves the stick of 8 cubes at me) and 9 (places the one I gave her on the top of the tower.)”
We brainstormed an activity that is fun and helps push student thinking. Teachers model it with a think aloud and then add it to their choice activities. You present a collection of interlocking chains that increase by one. How can I line up the chains in order from 1-10? How do I know which one comes next? Eventually, you can match each chain with a numeral. We ask the students what do you notice? Eventually, you can ask, “where do you see the one on the “two” chain?” You can do this with all sorts of collections.
Thanks for sharing.
Thanks for such a thoughtful and thorough comment. Your insight is super helpful.
There is definitely something to be said for videotaping student responses and discussing them as a team or grade level. Tons of ah-ha moments come from collaboration. All of us are smarter than one of us. Thanks for sharing!
Great video and lots of different ideas about how to move from counting to cardinality. I’ll be working with Pre-K and K teachers next month about this very topic. I’d love to use this video and have them share about different ways to answer the “Now what?” question. May I have permission to do that?
Absolutely Jana! Fire away and report back. I’d love to hear what your teachers have to say about helping Crosby out.
He might have cardinality for smaller numbers, so starting with a pile of 3 and asking “How many”, and then gradually increasing the quantity might be a good way to expand his understanding of the concept to larger amounts. Also, asking him to count out a quantity, and give you 3 or 5 or 7 from a larger amount might reinforce the idea as well. After he counts out the quantity you asked for, you can say, “Oh, so there are __?” Or, you can again relentlessly ask “How many are there?” 🙂
So, now that your own children have mastered counting and cardinality, you find someone else’s vulnerable lad to relentlessly question!? Love it.
The blessing and curse of loving what we do.
I did a lot of modeling that you can answer the “How many?” question with the last number said. With my 2 boys, we talked about the number of mittens we would need to get ready to go outside, the number of forks or plates, etc to set the table, the number of blocks we used in a tower… I would say, I wonder how many …. we used or we need and I would count the number of objects out loud and say, “One, two, three, four. Oh, so we need 4 forks to set the table.” I’d ask lots of how many questions as we emptied the dishwasher, folded the laundry, played with blocks and eventually it clicked 🙂 What stories of horror will our children of math teachers tell when they grow up? 🙂
I think there’s a lot to be said for consistent questioning. Nice simple examples of exposure kids to counting opportunities.
In terms of horror stories…we know they’re going to be some doozies!
My mom (note: NOT a math teacher at all) would use a backgammon board and we would play a game where we would have a race with 4 or 5 pieces from a pocket on one end to the pocket on the other using 1 die. I’ve used this strategy with several of my friends’ young children and have seen a lot of growth while we play. And it’s easy to ramp up the difficulty creating new rules to match learning. It’s fun as they first have to count all the pips on the die one-by-one but start to learn to recognize the numbers as they come up again and again:
“Oh, that’s 4!”
“How do you know?”
“Because that’s what 4 looks like.”
“Oh! Interesting.”
I also love the backgammon board because the points on the board act as a number line so they get to practice all sort of number sense skills.
And now I’m a HUGE backgammon nerd. (Nature? Nurture?) The patterns, differences, strategies, and choices are all rooted in number sense, probability, and expected value…and don’t get me started on the doubling cube!!!
But it’s an elegant way to introduce practice one-to-one (pips), cardinality, and number line.
Game play is a huge part in building the fluency because they providse opportunity to practice. I’m sure we could take many of the above suggestions and modify them into a game. I need to go back and identify potential games. Thanks Chase.
In terms of the dice recognition, there a difference between a perceptual and conceptual subitizer. Love the example you’ve shared of a perceptual subitizer.
Lol. Math teacher parents are the WORST!
No doubt!
Gorgeous! I have seen the same often around 3-4 years of age and have found that asking learners ‘mid-count’ (rather vaguely) “So, how many’s that so far…?” eventually helps them pay attention to the last number in the count, and then (tricky one!) to COUNT ON from that number. Eventually. At first they just start the count again just as your guy did. Love it. It amazes me how many times they ‘answer’ this question – after counting about 4 or 5 times, I have been told “All of these” or “Count them yourself!”
Kids are also much more accurate counters when they count into a container. Then you can pop the lid on and ask (you’ve guessed it) “So, how many is in there?”
These are all great questions Helen and I’m adding them to the question bank as I type. I really like the lid on the container idea because it in a way it models unitizing and hierarchal inclusion. Sweet!
Totally going to go and video my 4 year old now! Too cute! Have him count two different sets with different size objects, but they have the same number. 4 dogs versus 4 jelly-beans. Then discuss what was the same, what was different? Were you surprised they were the same? Why, why not? Another suggestion, count a set – now rearrange them…are they the same? why or why not?
Love the idea of scrambling objects around after counting and then asking “How many now?”
I’m interested to know what he’d say.
Try some “Are there more in this pile than in that pile” questions. This gets across the idea of “same number” as an abstraction from “same amount”.
Initially it doesn’t involve counting.
Will do and thanks as always Howard.
I love this video so much! Perfect. You caught him right in the moment.
Mine too. I love it when the he calls me out.
In my kinder intervention groups we used real items like pictures of their pets, flowers we picked, recess hula hoops, etc. We also played a hiding game where we put 3-6 real objects under a coat, they memorized them, we removed one or two, and they had to say which were gone. I felt like working with real items and in a game fashion supported the relevance of the questions being asked. While counting how many were missing or how many were still there worked to raise the relevance of the quantity for them. I am always looking for new ways to challenge the little ones that challenge me. 😉
Thanks Jamiee. I’ll definitely add this to my arsenal and give this a try.
I’m not sure, but one thing that worked well for my kids was involving them in counting – how many forks will we need? Counting blocks/ Legos/ Ponies/ rocks/ whatever. It seems like having kids count a lot and experiment with getting “stuff” is huge.
One thing that just dawned on me, and I’m not sure about it, is that there’s a difference between the counting sequence (we used to play a game called number pop at dinner – fun, right!?!) and counting to answer the question “How many?” That I’m sure of. What I’m unsure of is that families and teachers may emphasize the counting sequence, but not its application w/in quantity. So, I think one thing I’d want to encourage families to do is to provide children w/ opportunities to find “how many?” and “how many do we need?” Seems like that practice will lead to trusting number – or cardinality.
Great point Chris! There’s a lot to be said for attaching number names to physical quantities. Like if your driving down a country road and you see cows, you might say “Oh look, there’s some cows”. When you could say “Oh look, there’s 6 cows.”
I’ve watched the video a couple of times and it seems like the question “how many?” implies that an action needs to happen.
Any thoughts on a different question? I can see your point, but am not sure what else to ask.
In my district we used to talk about how a student had mastered or moved through a particular stage when they have you the, “Seriously? No duh!” look. In this case, a student who has moved from counting to cardinality might imply through body language, etc. “Seriously! I just told you there were 7! I. Am. Not. Counting. Them. Again!”
One task I’ve used to see if students “trust the number” is where I have a picture of 7 or so kids who ALL want ice cream. They’re really close together and look hungry. On another table, I have oversized cutouts of ice-cream cones. I ask the student to get enough ice cream so each child in the picture has one cone. Students who are still in the counting stage try to place the cone on each child. Sometimes they bring back too many, others not enough. Students who have moved on come back with the exact number and basically say, “Here.” They know there are enough because they counted the children in the picture and brought back the corresponding number of cones.
I always like the bucket activity. Count the items (1:1 correspondence) then put them in a bucket (or some other place where they can’t be counted again) and then ask again,”how many?” Forces that jump from counting to cardinality! Students can then re-check by using 1:1 correspondence by taking the items out of the bucket and re-counting.
It would make a great daily math routine for kindergarteners working on this move!
This would definitely help with the number retention piece. Thanks Andrew.